题目内容
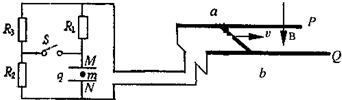
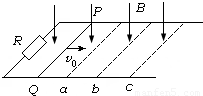 如图所示水平光滑的平行金属导轨,左端接有电阻R,匀强磁场B竖直向下分布在导轨所在空间内,质量一定的金属棒PQ垂直于导轨放置.今使棒以一定的初速度v向右运动,当其通过位置a.b时,速率分别为va.vb,到位置c时棒刚好静止.设导轨与棒的电阻均不计,a.b与b.c的间距相等,则金属棒在由a→b与b→c的两个过程中( )
如图所示水平光滑的平行金属导轨,左端接有电阻R,匀强磁场B竖直向下分布在导轨所在空间内,质量一定的金属棒PQ垂直于导轨放置.今使棒以一定的初速度v向右运动,当其通过位置a.b时,速率分别为va.vb,到位置c时棒刚好静止.设导轨与棒的电阻均不计,a.b与b.c的间距相等,则金属棒在由a→b与b→c的两个过程中( )A.棒运动的加速度相等
B.通过棒横截面的电量不相等
C.回路中产生的电能Eab=3Ebc
D.棒通过a.b两位置时速率关系为va>2vb
【答案】分析:根据题意,金属棒在向右运动过程中受到一个向左的安培力F,由于安培力F对金属棒做负功,所以金属棒的速度越来越小,加速度越来越小.
由感应电量q=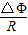 进行比较.
进行比较.
由a→b与b→c的两个过程中运用动量定理求解a.b两位置时速率关系.
a→b与b→c的两个过程中动能转化为电能,由能量守恒求解.
解答:解:A、由a→b和b→c,棒一直减速,回路中电流一直在减小,棒受安培力FA=BIl减小,
故加速度a= 减小,故A错误.
减小,故A错误.
B、金属棒在由a→b与b→c的两个过程中磁通量的变化量相同,
由感应电量q= 得通过棒横截面的电量相等,故B错误.
得通过棒横截面的电量相等,故B错误.
C、D、由动量定理知:从a→b,B 1l?△t1=mva-mvb,
1l?△t1=mva-mvb,
从b→c,B 2l?△t2=mvb-0
2l?△t2=mvb-0
而q1=q2即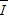 1△t1=
1△t1= 2△t2
2△t2
故有va=2vb,故D错误,
产生的电能由能量守恒有:Eab= -
- =
=
Ebc=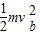 ,故C正确.
,故C正确.
故选C.
点评:本题考查综合运用电磁感应、电路知识、牛顿定律、动量定理等知识的能力.
由感应电量q=
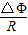 进行比较.
进行比较.由a→b与b→c的两个过程中运用动量定理求解a.b两位置时速率关系.
a→b与b→c的两个过程中动能转化为电能,由能量守恒求解.
解答:解:A、由a→b和b→c,棒一直减速,回路中电流一直在减小,棒受安培力FA=BIl减小,
故加速度a=
 减小,故A错误.
减小,故A错误.B、金属棒在由a→b与b→c的两个过程中磁通量的变化量相同,
由感应电量q=
 得通过棒横截面的电量相等,故B错误.
得通过棒横截面的电量相等,故B错误.C、D、由动量定理知:从a→b,B
 1l?△t1=mva-mvb,
1l?△t1=mva-mvb,从b→c,B
 2l?△t2=mvb-0
2l?△t2=mvb-0而q1=q2即
 1△t1=
1△t1= 2△t2
2△t2故有va=2vb,故D错误,
产生的电能由能量守恒有:Eab=
 -
- =
=
Ebc=
 ,故C正确.
,故C正确.故选C.
点评:本题考查综合运用电磁感应、电路知识、牛顿定律、动量定理等知识的能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图所示,光滑的曲面轨道的水平出口跟停在光滑水平面上的平板小车的上表面相平,质量为m的小滑块从光滑轨道上某处由静止开始滑下并滑下平板小车,使得小车在光滑水平面上滑动.已知小滑块从光滑轨道上高度为H的位置由静止开始滑下,最终停到板面上的Q点.若平板小车的质量为3m.用g表示本地的重力加速度大小,求:
如图所示,光滑的曲面轨道的水平出口跟停在光滑水平面上的平板小车的上表面相平,质量为m的小滑块从光滑轨道上某处由静止开始滑下并滑下平板小车,使得小车在光滑水平面上滑动.已知小滑块从光滑轨道上高度为H的位置由静止开始滑下,最终停到板面上的Q点.若平板小车的质量为3m.用g表示本地的重力加速度大小,求: (2011?奉贤区二模)如图所示,光滑的半圆柱体的半径为R,其上方有一个曲线轨道AB,轨道底端水平并与半圆柱体顶端相切.质量为m的小球沿轨道滑至底端(也就是半圆柱体的顶端)B点时的速度大小为
(2011?奉贤区二模)如图所示,光滑的半圆柱体的半径为R,其上方有一个曲线轨道AB,轨道底端水平并与半圆柱体顶端相切.质量为m的小球沿轨道滑至底端(也就是半圆柱体的顶端)B点时的速度大小为 如图所示,光滑绝缘平台上A点有质量为m=1kg的带电小物块,A、B间距离s=0.64m;质量为M=3kg、长为L=1m的不带电绝缘小车停在光滑水平地面上,且紧靠平台右侧,上表面与平台等高.此区间有E=2.5×103N/C的水平向右匀强电场,方向水平向右,t=0时刻小物块由静止开始向右运动,到达B处时撤去此电场,小物块由A至B过程中的动量满足条件Px=5.0
如图所示,光滑绝缘平台上A点有质量为m=1kg的带电小物块,A、B间距离s=0.64m;质量为M=3kg、长为L=1m的不带电绝缘小车停在光滑水平地面上,且紧靠平台右侧,上表面与平台等高.此区间有E=2.5×103N/C的水平向右匀强电场,方向水平向右,t=0时刻小物块由静止开始向右运动,到达B处时撤去此电场,小物块由A至B过程中的动量满足条件Px=5.0