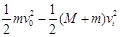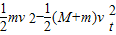题目内容
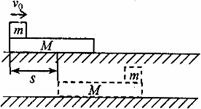
一质量为M的长木板静止在光滑水平桌面上.一质量为m的小滑块以水平速度v0从长木板的一端开始在木板上滑动,直到离开木板.滑块刚离开木板时的速度为v0/3.若把该木板固定在水平桌面上,其它条件相同,求滑块离开木板时的速度v.
分析:木板在光滑桌面上滑动时滑块和木板的动量守恒,根据动量守恒定律可求出第一次滑块离开时木板速度;
由动能定理对木板和滑块分别研究列出等式,再研究当板固定时运用动能定理求解滑块离开木板时的速度.
由动能定理对木板和滑块分别研究列出等式,再研究当板固定时运用动能定理求解滑块离开木板时的速度.
解答:解:设第一次滑块离开时木板速度为v,由系统的动量守恒,有
mvo=m?
+Mv,
解得v=
设滑块与木板间摩擦力为f,木板长L,滑行距离s,如图,
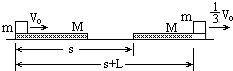
由动能定理对木板:fs=
Mv2
对滑块:-f(s+L)=
m(
)2-
m
即 fL=
m
-
m(
)2-
Mv2
当板固定时 fL=
m
-
mv′2
解得 v′=
答:滑块离开木板时的速度大小是
mvo=m?
| v0 |
| 3 |
解得v=
| 2mv0 |
| 3M |
设滑块与木板间摩擦力为f,木板长L,滑行距离s,如图,

由动能定理对木板:fs=
| 1 |
| 2 |
对滑块:-f(s+L)=
| 1 |
| 2 |
| v0 |
| 3 |
| 1 |
| 2 |
| v | 2 0 |
即 fL=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v0 |
| 3 |
| 1 |
| 2 |
当板固定时 fL=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
解得 v′=
| v0 |
| 3 |
1+
|
答:滑块离开木板时的速度大小是
| v0 |
| 3 |
1+
|
点评:当遇到相互作用的问题时,要想到应用动量守恒定律;
一个题目可能选择不同的研究对象运用动能定理求解,要注意求解功时的位移是物体相对于地面的位移.
一个题目可能选择不同的研究对象运用动能定理求解,要注意求解功时的位移是物体相对于地面的位移.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
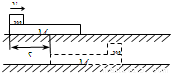
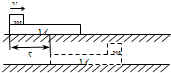 如图所示,质量为M的长木板静置于光滑水平面上,一质量为m的小铅块(可视为质点)以水平初速v0由木板左端滑上木板,铅块滑至木板的右端时恰好与木板相对静止,此时,它们共同的速度为vt.已知铅块与长木板间的动摩擦因数为μ,木板长为L,在此过程中,木板前进的距离为s.则在这个过程中铅块克服摩擦力所做的功等于( )
如图所示,质量为M的长木板静置于光滑水平面上,一质量为m的小铅块(可视为质点)以水平初速v0由木板左端滑上木板,铅块滑至木板的右端时恰好与木板相对静止,此时,它们共同的速度为vt.已知铅块与长木板间的动摩擦因数为μ,木板长为L,在此过程中,木板前进的距离为s.则在这个过程中铅块克服摩擦力所做的功等于( )