题目内容
[物理--选修3-5](1)下面列出的是两个核反应方程式,X1和X2各代表某种粒子.
①
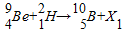
②
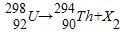
则以下判断中正确的是______
A.X1是电子,X2是α粒子 B.X1是中子,X2是质子
C.X1是质子,X2是中子 D.X1是中子,X2是α粒子
(2)云室处在磁感应强度为B的匀强磁场中,一静止的质量为M的原子核在云室中发生一次α衰变.α粒子的质量为m,带电量为q,其运动轨迹在与磁场垂直的平面内.现测得α粒子运动的迹道半径为R,试求在衰变过程中的质量亏损(涉及动量问题时,亏损的质量可忽略不计).
【答案】分析:(1)核反应过程质量数与核电荷数守恒,据此分析答题.
(2)粒子在磁场中做圆周运动,由牛顿第二定律求出粒子速度,
衰变过程中动量守恒,由动量守恒定律可以求出另外一个粒子的速度,
由质能方程求出质量亏损.
解答:解:(1)由质量数守恒与核电荷数守恒可知,
x1的和核电荷数为0,质量数为1,则x1为中子;
x2的核电荷数为2,质量数为4,则x2为α粒子,
故选D.
(2)该衰变放出的α粒子在匀强磁场中做匀速圆周运动,
其轨道半径R与运动速度v的关系,
由洛仑兹力和牛顿定律得:qvB=m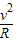 ,
,
由衰变过程动量守恒得:mv+(M-m)v′=0,又衰变过程中,能量守恒,则粒子和剩余核的动能都来自于亏损质量,
△mc2= mv2+
mv2+ (M-m)v′2,
(M-m)v′2,
解得△m= ;
;
故答案为:(1)D;
(2)衰变过程中的质量亏损为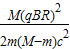 .
.
点评:衰变后粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出粒子的速度.
(2)粒子在磁场中做圆周运动,由牛顿第二定律求出粒子速度,
衰变过程中动量守恒,由动量守恒定律可以求出另外一个粒子的速度,
由质能方程求出质量亏损.
解答:解:(1)由质量数守恒与核电荷数守恒可知,
x1的和核电荷数为0,质量数为1,则x1为中子;
x2的核电荷数为2,质量数为4,则x2为α粒子,
故选D.
(2)该衰变放出的α粒子在匀强磁场中做匀速圆周运动,
其轨道半径R与运动速度v的关系,
由洛仑兹力和牛顿定律得:qvB=m
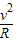 ,
,由衰变过程动量守恒得:mv+(M-m)v′=0,又衰变过程中,能量守恒,则粒子和剩余核的动能都来自于亏损质量,
△mc2=
 mv2+
mv2+ (M-m)v′2,
(M-m)v′2,解得△m=
 ;
; 故答案为:(1)D;
(2)衰变过程中的质量亏损为
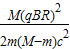 .
.点评:衰变后粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出粒子的速度.

练习册系列答案
相关题目
 (2)如图,小车质量为M=2.0kg,带有光滑的圆弧轨道AB和粗糙的水平轨道BC,一小物块(可视为质点)质量为m=0.5kg,与轨道BC的动摩擦因数为μ=0.10,BC部分总长度为L=0.80m.重力加速度g取10m/s2.
(2)如图,小车质量为M=2.0kg,带有光滑的圆弧轨道AB和粗糙的水平轨道BC,一小物块(可视为质点)质量为m=0.5kg,与轨道BC的动摩擦因数为μ=0.10,BC部分总长度为L=0.80m.重力加速度g取10m/s2. 物理--选修3-5
物理--选修3-5 (物理-选修3-5)
(物理-选修3-5)
 (2011?长春二模)[物理--选修3-5]
(2011?长春二模)[物理--选修3-5]