题目内容
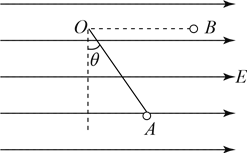
【题目】如图是倾角为θ的斜坡,在斜坡底端P点正上方的某一点Q处以速度v0水平向左抛出一个小球A,同时从Q由静止释放另一小球B.已知小球A恰好垂直落在斜坡上,不计空气阻力,求:
(1)A落在斜坡上的M位置与P的距离;
(2)A落在斜坡上时再经多长时间小球B能到达P点?
【答案】
(1)
解:小球A落到斜坡上M点经历时间为t.
则小球A落在斜面上时竖直分速度为 vy=gt
因为A球恰好垂直落在斜坡上时速度与斜坡垂直,则 ![]()
水平位移 xM=v0t
由几何关系有: ![]()
(2)
解:两球落地前竖直方向运动情况是一样的,设A落在斜坡上M点后经历时间△t小球B到P点:hMP=xMtanθ
由 ![]() 得:
得: ![]()
【解析】(1)小球A做平抛运动时,恰好垂直落在斜坡上时速度与斜坡垂直,根据速度的分解,求出运动的时间,然后求出水平位移,根据几何关系求解.(2)根据数学知识求出MP间的距离,两球落地前竖直方向运动情况是一样的,再根据匀加速直线运动的位移时间公式求解时间.
【考点精析】解答此题的关键在于理解平抛运动的相关知识,掌握特点:①具有水平方向的初速度;②只受重力作用,是加速度为重力加速度g的匀变速曲线运动;运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.

练习册系列答案
相关题目