题目内容
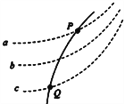
【题目】如图为验证动量守恒定律的实验装置，实验中选取两个半径相同、质量不等的小球，按下面步骤进行实验：
①用天平测出两个小球的质量分别为m1和m2；
②安装实验装置，将斜槽AB固定在桌边，使槽的末端切线水平，再将一斜面BC连接在斜槽末端；
③先不放小球m2 ， 让小球m1从斜槽顶端A处由静止释放，标记小球在斜面上的落点位置P；
④将小球m2放在斜槽末端B处，仍让小球m1从斜槽顶端A处由静止释放，两球发生碰撞，分别标记小球m1、m2在斜面上的落点位置；
⑤用毫米刻度尺测出各落点位置到斜槽末端B的距离．图中从M、P、N点是实验过程中记下的小球在斜面上的三个落点位置，从M、P、N到B点的距离分别为SM、SP、SN ． 依据上述实验步骤，请回答下面问题：
（1）两小球的质量m1、m2应满足m1m2（填写“＞”、“=”或“＜”）；
（2）小球m1与m2发生碰撞后，m1的落点是图中点，m2的落点是图中点；
（3）用实验中测得的数据来表示，只要满足关系式 ， 就能说明两球碰撞前后动量是守恒的；
（4）若要判断两小球的碰撞是否为弹性碰撞，用实验中测得的数据来表示，只需比较与是否相等即可．
【答案】
（1）＞
（2）M,N
（3）m1 
=m1 
+m2 
（4）m1SP,m1SM+m2SN
【解析】解：（1）为了防止入射球碰后反弹，一定要保证入射球的质量大于被碰球的质量；（2）小球m1和小球m2相撞后，小球m2的速度增大，小球m1的速度减小，都做平抛运动，所以碰撞后m1球的落地点是M点，m2球的落地点是N点；（3）碰撞前，小于m1落在图中的P点，设其水平初速度为v1．小球m1和m2发生碰撞后，m1的落点在图中的M点，设其水平初速度为v1′，m2的落点是图中的N点，设其水平初速度为v2． 设斜面BC与水平面的倾角为α，
由平抛运动规律得：SMsinα= 
gt2，SMcosα=v′1t
解得：v1'= 
同理可解得：v1= 
，v2= 
所以只要满足m1v1=m2v2+m1v′1即：m1 =m1 +m2 则说明两球碰撞过程中动量守恒；
如果满足小球的碰撞为弹性碰撞，则应满足：
m1v1'2= m1v12+ m2v22
代入以上速度表达式可知，应满足公式为：
m1SP=m1SM+m2SN；
故需要验证：m1SP和m1SM+m2SN相等．
所以答案是：（1）＞（2）M；N；（3）m1 =m1 +m2 ；（4）m1SP；m1SM+m2SN；
