题目内容
16. 如图,一质量为m=10kg的物体,由$\frac{1}{4}$光滑圆弧轨道上端从静止开始下滑,到达底端后沿水平面向右滑动2m距离后停止.已知轨道半径R=0.8m,g=10m/s2,求:
如图,一质量为m=10kg的物体,由$\frac{1}{4}$光滑圆弧轨道上端从静止开始下滑,到达底端后沿水平面向右滑动2m距离后停止.已知轨道半径R=0.8m,g=10m/s2,求:(1)物体滑至圆弧底端时的速度大小
(2)物体滑至圆弧底端时对轨道的压力大小
(3)物体沿水平面滑动过程中的动摩擦因数μ
分析 (1)物体在光滑圆弧轨道上下滑过程,只有重力做功,根据动能定理列式求解;
(2)在圆弧底端时,合力提供向心力,根据牛顿第二定律列式求解;
(3)应用动能定理可以求出动摩擦因数.
解答 解:(1)物体在光滑圆弧轨道上下滑过程,根据动能定理有:
mgR=$\frac{1}{2}$mv2-0,
解得:v=$\sqrt{2gR}$=$\sqrt{2×10×0.8}$=4m/s;
(2)在圆弧底端时,受重力和支持力,根据牛顿第二定律,有:
FN-mg=m$\frac{{v}^{2}}{R}$,
解得:FN=mg+m$\frac{{v}^{2}}{R}$=10×10+10×$\frac{{4}^{2}}{0.8}$=300N,
根据牛顿第三定律,物体对轨道的压力大小为300N;
(3)对整个过程,由动能定理得:
mgR-μmgs=0-0,
解得:μ=$\frac{R}{s}$=$\frac{0.8}{2}$=0.4;
答:(1)物体滑至圆弧底端时的速度大小4m/s;
(2)物体滑至圆弧底端时对轨道的压力大小300N;
(3)物体沿水平面滑动过程中的动摩擦因数μ为0.4.
点评 本题是动能定理和向心力公式的运用问题,动能定理不仅适用于直线运动,而且适用与曲线运动,对单个过程和多过程均适用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.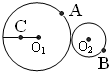 如图所示,A、B两点分别位于大小两轮O1、O2的边缘上,C点位于大轮O1半径的中点,大轮半径是小轮的2倍,它们之间靠摩擦传动,接触面不打滑.在两轮转动时,对于A、B、C三点的线速度和角速度,以下关系成立的是( )
如图所示,A、B两点分别位于大小两轮O1、O2的边缘上,C点位于大轮O1半径的中点,大轮半径是小轮的2倍,它们之间靠摩擦传动,接触面不打滑.在两轮转动时,对于A、B、C三点的线速度和角速度,以下关系成立的是( )
 如图所示,A、B两点分别位于大小两轮O1、O2的边缘上,C点位于大轮O1半径的中点,大轮半径是小轮的2倍,它们之间靠摩擦传动,接触面不打滑.在两轮转动时,对于A、B、C三点的线速度和角速度,以下关系成立的是( )
如图所示,A、B两点分别位于大小两轮O1、O2的边缘上,C点位于大轮O1半径的中点,大轮半径是小轮的2倍,它们之间靠摩擦传动,接触面不打滑.在两轮转动时,对于A、B、C三点的线速度和角速度,以下关系成立的是( )| A. | vA:vB:vC=1:1:1 | B. | vA:vB:vC=2:2:1 | C. | ωA:ωB:ωC=1:1:2 | D. | ωA:ωB:ωC=1:2:1 |
4.关于地球同步卫星,下列说法正确的是( )
| A. | 它的周期与地球自转周期相同,但高度和速度可以选择 | |
| B. | 它的绕行方向可以与地球自转方向相反 | |
| C. | 我国发射的同步卫星可以定点在北京上空 | |
| D. | 我国发射的同步卫星必须定点在赤道上空 |
11.一质量为m的物体放在水平面上,在水平推力F的作用下做匀速直线运动,物体与水平面间的动摩擦因数为μ,则物体所受摩擦力( )
| A. | f=μmg | B. | F | C. | f=μF | D. | f=μmg+F |
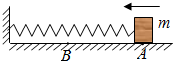 如图所示,质量为0.4kg的物块以速度3.0m/s在A点碰上一轻弹簧,弹簧的另一端固定,木块碰上弹簧后,使弹簧的最大压缩量为0.2m.物块与水平地面的动摩擦因数为0.25.重力加速度为g=10m/s2.求
如图所示,质量为0.4kg的物块以速度3.0m/s在A点碰上一轻弹簧,弹簧的另一端固定,木块碰上弹簧后,使弹簧的最大压缩量为0.2m.物块与水平地面的动摩擦因数为0.25.重力加速度为g=10m/s2.求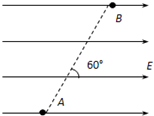 如图所示,在匀强电场中,将一电荷量为2×10-5C的正电荷由A点移到B点,其电势能减少了0.1J,已知A、B两点间距离为2cm,两点连线与电场方向成60°角,求:
如图所示,在匀强电场中,将一电荷量为2×10-5C的正电荷由A点移到B点,其电势能减少了0.1J,已知A、B两点间距离为2cm,两点连线与电场方向成60°角,求: