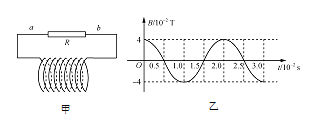
题目内容
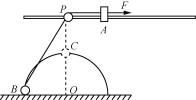
【题目】如图所示,竖直平面内有一固定绝缘轨道ABCDP,由半径r=0.5m的圆弧轨道CDP和与之相切于C点的水平轨道ABC组成,圆弧轨道的直径DP与竖直半径OC间的夹角θ=37°,A、B两点间的距离d=0.2m。质量m1=0.05kg的不带电绝缘滑块静止在A点,质量m2=0.1kg、电荷量q=1×10-5C的带正电小球静止在B点,小球的右侧空间存在水平向右的匀强电场。现用大小F=4.5N、方向水平向右的恒力推滑块,滑块到达月点前瞬间撤去该恒力,滑块与小球发生弹性正碰,碰后小球沿轨道运动,到达P点时恰好和轨道无挤压且所受合力指向圆心。小球和滑块均视为质点,碰撞过程中小球的电荷量不变,不计一切摩擦。取g=10m/s2,sin37°=0.6,cos37°=0.8。

(1)求撤去该恒力瞬间滑块的速度大小v以及匀强电场的电场强度大小E;
(2)求小球到达P点时的速度大小vP和B、C两点间的距离x。
【答案】(1) 6m/s;7.5×104N/C (2) 2.5m/s ;0.85m
【解析】
(1)对滑块从A点运动到B点的过程,根据动能定理有:![]()
解得:v=6m/s
小球到达P点时,受力如图所示:
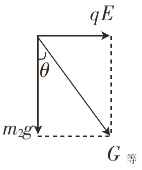
则有:qE=m2gtanθ,
解得:E=7.5×104N/C
(2)小球所受重力与电场力的合力大小为:![]()
小球到达P点时,由牛顿第二定律有:![]()
解得:vP=2.5m/s
滑块与小球发生弹性正碰,设碰后滑块、小球的速度大小分别为v1、v2,
则有:m1v=m1v1+m2v2
![]()
解得:v1=-2m/s(“-”表示v1的方向水平向左),v2=4m/s
对小球碰后运动到P点的过程,根据动能定理有:![]()
解得:x=0.85m

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目