题目内容
 把一个质量为0.1kg的小球用细线悬挂起来,就成为一个摆.如图,摆长为0.9米,当偏角θ为60°时,释放小球,如果阻力可以忽略,求:
把一个质量为0.1kg的小球用细线悬挂起来,就成为一个摆.如图,摆长为0.9米,当偏角θ为60°时,释放小球,如果阻力可以忽略,求:(1)小球运动到最低位置O时的速度是多大?
(2)小球运动到最低位置O时,细线对小球的拉力是多大?
(3)假设摆的下方是一个倾角为45°的斜面,如果小球运动到位置O时,恰好细线断了,若OD间距离h=6.75米,求小球落地点P到O点正下方的斜面上D点的距离是多少?
分析:(1)小球在摆动的过程中,只有重力做功,机械能守恒,根据机械能守恒定律求出小球运动到最低位置O时的速度大小.
(2)在最低点O时,小球靠重力和拉力的合力提供向心力,根据牛顿第二定律求出细线的拉力大小.
(3)小球运动到位置O时恰好细线断了,此后小球做平抛运动,设小球落地点P到O点的水平距离为x,竖直距离为y,根据平抛运动的规律得到x和y的表达式,再根据数学知识得到:h-y=x,即可求得x和y,再根据几何知识求出P到斜面上D点的距离.
(2)在最低点O时,小球靠重力和拉力的合力提供向心力,根据牛顿第二定律求出细线的拉力大小.
(3)小球运动到位置O时恰好细线断了,此后小球做平抛运动,设小球落地点P到O点的水平距离为x,竖直距离为y,根据平抛运动的规律得到x和y的表达式,再根据数学知识得到:h-y=x,即可求得x和y,再根据几何知识求出P到斜面上D点的距离.
解答:解(1)由偏角θ为60°释放小球到最低点时,竖直的高度差是:
h=l(1-cos60°)=0.9×(1-0.5)m=0.45m
此过程,根据机械能守恒定律知:mgh=
mv2
所以有:v=
=
m/s=3m/s
(2)在最低点O,合外力提供向心力,有:F合=F向
则得:F拉-mg=
解得:F拉=mg+
=mg+2mg(1-cos60°)=2mg=2×0.2×10N=4N
(3)设小球落地点P到O点的水平距离为x,竖直距离为y,则有:
x=vt
y=
gt2
由于斜面的倾角为45°,根据数学知识得知:h-y=x
联立得:h-
gt2=vt
代入得:6.75-5t2=3t
解得:t=1.5s(另一值为负,舍去)
则P到O点正下方的斜面上D点的距离是 s=
x=
vt=
×3×1.5=
m
答:(1)小球运动到最低位置O时的速度是3m/s;
(2)小球运动到最低位置O时,细线对小球的拉力是4N;
(3)假设摆的下方是一个倾角为45°的斜面,如果小球运动到位置O时,恰好细线断了,若OD间距离h=6.75米,求小球落地点P到O点正下方的斜面上D点的距离是
m.
h=l(1-cos60°)=0.9×(1-0.5)m=0.45m
此过程,根据机械能守恒定律知:mgh=
| 1 |
| 2 |
所以有:v=
| 2gl(1-cos60°) |
| 2×10×0.9×0.5 |
(2)在最低点O,合外力提供向心力,有:F合=F向
则得:F拉-mg=
| mv2 |
| l |
解得:F拉=mg+
| mv2 |
| l |
(3)设小球落地点P到O点的水平距离为x,竖直距离为y,则有:
x=vt
y=
| 1 |
| 2 |
由于斜面的倾角为45°,根据数学知识得知:h-y=x
联立得:h-
| 1 |
| 2 |
代入得:6.75-5t2=3t
解得:t=1.5s(另一值为负,舍去)
则P到O点正下方的斜面上D点的距离是 s=
| 2 |
| 2 |
| 2 |
9
| ||
| 2 |
答:(1)小球运动到最低位置O时的速度是3m/s;
(2)小球运动到最低位置O时,细线对小球的拉力是4N;
(3)假设摆的下方是一个倾角为45°的斜面,如果小球运动到位置O时,恰好细线断了,若OD间距离h=6.75米,求小球落地点P到O点正下方的斜面上D点的距离是
9
| ||
| 2 |
点评:本题综合考查了机械能守恒定律、牛顿第二定律和平抛运动,关键是根据几何知识分析平抛运动两个分位移的关系,求解平抛运动的时间,有一定的难度,需加强这方面的训练,提高解题能力.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
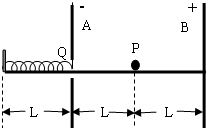 如图所示,A、B是两块竖直放置的平行金属板,相距为2L,分别带有等量的负、正电荷,在两板间形成电场强度大小为E的匀强电场.A板上有一小孔(它的存在对两板间匀强电场分布的影响可忽略不计),孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道,一个质量为m,电荷量为g(g>0)的小球(可视为质点),在外力作用下静止在轨道的中点P处.孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道,轨道上距A板L处有一固定档板,长为L的轻弹簧左端固定在挡板上,右端固定一块轻小的绝缘材料制成的薄板Q.撤去外力释放带电小粒,它将在电场力作用下由静止开始向左运动,穿过小孔后(不与金属板A接触)与薄板Q一起压缩弹簧,由于薄板Q及弹簧的质量都可以忽略不计,可认为小球与Q接触过程中不损失机械能.小球从接触Q开始,经历时间To第一次把弹簧压缩至最短,然后又被弹簧弹回.由于薄板Q的绝缘性能有所欠缺,使得小球每次离开Q瞬间,小球的电荷量都损失一部分,而变成刚与Q接触时小球电荷量的
如图所示,A、B是两块竖直放置的平行金属板,相距为2L,分别带有等量的负、正电荷,在两板间形成电场强度大小为E的匀强电场.A板上有一小孔(它的存在对两板间匀强电场分布的影响可忽略不计),孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道,一个质量为m,电荷量为g(g>0)的小球(可视为质点),在外力作用下静止在轨道的中点P处.孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道,轨道上距A板L处有一固定档板,长为L的轻弹簧左端固定在挡板上,右端固定一块轻小的绝缘材料制成的薄板Q.撤去外力释放带电小粒,它将在电场力作用下由静止开始向左运动,穿过小孔后(不与金属板A接触)与薄板Q一起压缩弹簧,由于薄板Q及弹簧的质量都可以忽略不计,可认为小球与Q接触过程中不损失机械能.小球从接触Q开始,经历时间To第一次把弹簧压缩至最短,然后又被弹簧弹回.由于薄板Q的绝缘性能有所欠缺,使得小球每次离开Q瞬间,小球的电荷量都损失一部分,而变成刚与Q接触时小球电荷量的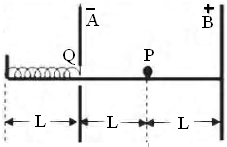 如图所示,A、B是两块竖直放置的平行金属板,相距为2L,分别带有等量的正、负电荷,在两板间形电场强度大小为E匀强电场.A板上有一小孔(它的存在对两板间匀强电场分布的影响可忽略不计),孔中有一条与板垂直的水平光滑绝缘轨道,一个质量为m,电荷量为q(q>0)的小球(可视为质点),在外力作用下静止在轨道的中点P处.一自然长度为L的轻弹簧左端固定在距A板左侧L处挡板上,右端固定一块轻小的绝缘材料制成的薄板Q.撤去外力释放带电小球,它将在电场力作用下由静止开始向左运动,穿过小孔后(不与金属板A接触)与薄板Q一起压缩弹簧,由于薄板Q及弹簧的质量都可以忽略不计,可认为小球与Q接触过程中不损失机械能.小球从接触Q开始,经过一段时间第一次把弹簧压缩至最短,然后又被弹簧弹回.由于薄板Q的绝缘性能有所欠缺,使得小球每次离开Q瞬间,小球的电荷量都损失一部分,而变成刚与Q接触时小球电荷量的
如图所示,A、B是两块竖直放置的平行金属板,相距为2L,分别带有等量的正、负电荷,在两板间形电场强度大小为E匀强电场.A板上有一小孔(它的存在对两板间匀强电场分布的影响可忽略不计),孔中有一条与板垂直的水平光滑绝缘轨道,一个质量为m,电荷量为q(q>0)的小球(可视为质点),在外力作用下静止在轨道的中点P处.一自然长度为L的轻弹簧左端固定在距A板左侧L处挡板上,右端固定一块轻小的绝缘材料制成的薄板Q.撤去外力释放带电小球,它将在电场力作用下由静止开始向左运动,穿过小孔后(不与金属板A接触)与薄板Q一起压缩弹簧,由于薄板Q及弹簧的质量都可以忽略不计,可认为小球与Q接触过程中不损失机械能.小球从接触Q开始,经过一段时间第一次把弹簧压缩至最短,然后又被弹簧弹回.由于薄板Q的绝缘性能有所欠缺,使得小球每次离开Q瞬间,小球的电荷量都损失一部分,而变成刚与Q接触时小球电荷量的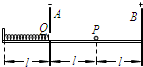 如图所示,A、B是两块竖直放置的平行金属板,相距为2l,分别带有等量的负、正电荷,在两板间形成电场强度大小为E的匀强电场.A板上有一小孔(它的存在对两板间匀强电场分布的影响可忽略不计),孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道,一个质量为m、电荷量为q(q>0)的小球(可视为质点),在外力作用下静止在轨道的中点P处.孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道,轨道上距A板l处有一固定档板,长为l的轻弹簧左端固定在挡板上,右端固定一块轻小的绝缘材料制成的薄板Q.撤去外力释放带电小球,它将在电场力作用下由静止开始向左运动,穿过小孔(不与金属板A接触)后与薄板Q一起压缩弹簧,由于薄板Q及弹簧的质量都可以忽略不计,可认为小球与Q接触过程中不损失机械能.小球从接触Q开始,经历时间T0第一次把弹簧压缩至最短,然后又被弹簧弹回.由于薄板Q的绝缘性能有所欠缺,使得小球每次离开弹簧的瞬间,小球的电荷量都损失一部分,而变成刚与弹簧接触时小球电荷量的
如图所示,A、B是两块竖直放置的平行金属板,相距为2l,分别带有等量的负、正电荷,在两板间形成电场强度大小为E的匀强电场.A板上有一小孔(它的存在对两板间匀强电场分布的影响可忽略不计),孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道,一个质量为m、电荷量为q(q>0)的小球(可视为质点),在外力作用下静止在轨道的中点P处.孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道,轨道上距A板l处有一固定档板,长为l的轻弹簧左端固定在挡板上,右端固定一块轻小的绝缘材料制成的薄板Q.撤去外力释放带电小球,它将在电场力作用下由静止开始向左运动,穿过小孔(不与金属板A接触)后与薄板Q一起压缩弹簧,由于薄板Q及弹簧的质量都可以忽略不计,可认为小球与Q接触过程中不损失机械能.小球从接触Q开始,经历时间T0第一次把弹簧压缩至最短,然后又被弹簧弹回.由于薄板Q的绝缘性能有所欠缺,使得小球每次离开弹簧的瞬间,小球的电荷量都损失一部分,而变成刚与弹簧接触时小球电荷量的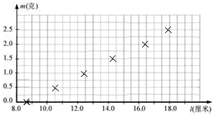 (2011?安徽)Ⅰ.为了测量某一弹簧的劲度系数,将该弹簧竖直悬挂起来,在自由端挂上不同质量的砝码.实验测了砝码的质量m与弹簧长度l的相应数据,对应点已在图上标出.(g=9.8m/s2)
(2011?安徽)Ⅰ.为了测量某一弹簧的劲度系数,将该弹簧竖直悬挂起来,在自由端挂上不同质量的砝码.实验测了砝码的质量m与弹簧长度l的相应数据,对应点已在图上标出.(g=9.8m/s2)