题目内容
11.一小轿车在一路口掉头行驶,速度为v=5m/s,这是轿车司机发现后面有一货车高速驶来,其速度为v′=20m/s,两者间的距离为L=30m.a′=0.25m/s2的加速度减速,为避免相撞,轿车至少应以多大的加速度行驶?分析 抓住两者恰好不相撞,此时速度相等,结合位移关系,运用运动学公式求出轿车的最小加速度.
解答 解:假设两者恰不相撞时轿车的加速度为a,经过t时间两者速度相等,此时两者恰好相遇,则:
v+at=v′-a′t,
s轿+L=s货,
根据匀变速直线运动的规律得:
${s}_{轿}=vt+\frac{1}{2}a{t}^{2}$,${s}_{货}=v′t-\frac{1}{2}a′{t}^{2}$,
代入数据联立解得:t=4s,a=3.5m/s2.
答:为避免相撞,轿车至少应以3.5m/s2的加速度行驶.
点评 本题考查了运动学中的追及相遇问题,关键抓住位移关系,结合临界状态,即速度相等时恰好不相撞,运用运动学公式进行求解,难度不大.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
5.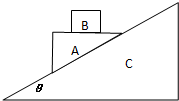 如图所示,光滑固定斜面C倾角为θ,质量均为m的A、B一起以某一初速沿斜面向上做匀减速运动,已知A上表面是水平的.则下列正确的是( )
如图所示,光滑固定斜面C倾角为θ,质量均为m的A、B一起以某一初速沿斜面向上做匀减速运动,已知A上表面是水平的.则下列正确的是( )
 如图所示,光滑固定斜面C倾角为θ,质量均为m的A、B一起以某一初速沿斜面向上做匀减速运动,已知A上表面是水平的.则下列正确的是( )
如图所示,光滑固定斜面C倾角为θ,质量均为m的A、B一起以某一初速沿斜面向上做匀减速运动,已知A上表面是水平的.则下列正确的是( )| A. | A受到B的摩擦力水平向右 | B. | B受到A的支持力不做功 | ||
| C. | B的机械能不变 | D. | A、B之间的摩擦力为mgsinθcosθ |
6. 如图所示,O、B、A为一粗糙绝缘水平面上的三点,一电荷量为-Q的点电荷固定在O点,现有一质量为m,电荷量为+q的小金属块(可视为质点),从A点以初速度v0沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为v.已知小金属块与水平面间的动摩擦因数为μ、AB间距离为L、静电力常量为k,则( )
如图所示,O、B、A为一粗糙绝缘水平面上的三点,一电荷量为-Q的点电荷固定在O点,现有一质量为m,电荷量为+q的小金属块(可视为质点),从A点以初速度v0沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为v.已知小金属块与水平面间的动摩擦因数为μ、AB间距离为L、静电力常量为k,则( )
 如图所示,O、B、A为一粗糙绝缘水平面上的三点,一电荷量为-Q的点电荷固定在O点,现有一质量为m,电荷量为+q的小金属块(可视为质点),从A点以初速度v0沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为v.已知小金属块与水平面间的动摩擦因数为μ、AB间距离为L、静电力常量为k,则( )
如图所示,O、B、A为一粗糙绝缘水平面上的三点,一电荷量为-Q的点电荷固定在O点,现有一质量为m,电荷量为+q的小金属块(可视为质点),从A点以初速度v0沿它们的连线向固定点电荷运动,到B点时速度最小,其大小为v.已知小金属块与水平面间的动摩擦因数为μ、AB间距离为L、静电力常量为k,则( )| A. | OB间的距离为$\sqrt{\frac{kQq}{μmg}}$ | |
| B. | 在小金属块由A向O运动的过程中,电势能先增大后减小 | |
| C. | 在小金属块由A向O运动的过程中,其加速度先减小后增大 | |
| D. | 在点电荷-Q形成的电场中,A、B两点间的电势差为$\frac{μmgL+\frac{1}{2}m{v}^{2}}{q}$ |
3. 如图中的实线表示电场线,虚线表示只受电场力作用时正电荷的运动轨迹,电荷从M点运动到N点,下列说法中正确的有( )
如图中的实线表示电场线,虚线表示只受电场力作用时正电荷的运动轨迹,电荷从M点运动到N点,下列说法中正确的有( )
 如图中的实线表示电场线,虚线表示只受电场力作用时正电荷的运动轨迹,电荷从M点运动到N点,下列说法中正确的有( )
如图中的实线表示电场线,虚线表示只受电场力作用时正电荷的运动轨迹,电荷从M点运动到N点,下列说法中正确的有( )| A. | M点的电势大于N点的电势 | |
| B. | M点的电势小于N点的电势 | |
| C. | M点的动能小于N点的动能 | |
| D. | 粒子在M点受到的电场力小于在N点受到的电场力 |
20.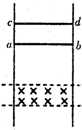 如图所示,匀强磁场边界水平,方向垂直纸面向里,两固定竖直光滑金属导轨电阻不计,完全相同的导体棒ab、cd水平置于磁场上方且相距一定距离.现同时由静止释放ab、cd,ab进入磁场时恰好做匀速运动,ab出磁场时,cd刚好进入磁场,已知导体棒与导轨接触良好.竖直导轨足够长,则cd在穿越磁场过程中( )
如图所示,匀强磁场边界水平,方向垂直纸面向里,两固定竖直光滑金属导轨电阻不计,完全相同的导体棒ab、cd水平置于磁场上方且相距一定距离.现同时由静止释放ab、cd,ab进入磁场时恰好做匀速运动,ab出磁场时,cd刚好进入磁场,已知导体棒与导轨接触良好.竖直导轨足够长,则cd在穿越磁场过程中( )
 如图所示,匀强磁场边界水平,方向垂直纸面向里,两固定竖直光滑金属导轨电阻不计,完全相同的导体棒ab、cd水平置于磁场上方且相距一定距离.现同时由静止释放ab、cd,ab进入磁场时恰好做匀速运动,ab出磁场时,cd刚好进入磁场,已知导体棒与导轨接触良好.竖直导轨足够长,则cd在穿越磁场过程中( )
如图所示,匀强磁场边界水平,方向垂直纸面向里,两固定竖直光滑金属导轨电阻不计,完全相同的导体棒ab、cd水平置于磁场上方且相距一定距离.现同时由静止释放ab、cd,ab进入磁场时恰好做匀速运动,ab出磁场时,cd刚好进入磁场,已知导体棒与导轨接触良好.竖直导轨足够长,则cd在穿越磁场过程中( )| A. | d端电势高于c端 | |
| B. | 匀速穿过磁场 | |
| C. | 运动时间小于ab在磁场中运动时间 | |
| D. | 克服安培力做的功等于ab穿越磁场过程中克服安培力做的功 |
1.下列关于物体运动的一些说法中,哪些是可能的( )
| A. | 速度变化的方向为正,加速度方向为负 | |
| B. | 物体的加速度大小不变,其速度在减小 | |
| C. | 物体的速度为零,而加速度很大 | |
| D. | 物体的加速度跟速度方向相同时,当加速度减小,速度也随之减小 |
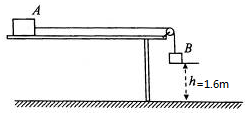 如图所示,物块A与水平面之间的动摩擦因数为μ=0.2,物块A、B的质量分别为5kg、3kg,不计绳子的质量和滑轮摩擦,则
如图所示,物块A与水平面之间的动摩擦因数为μ=0.2,物块A、B的质量分别为5kg、3kg,不计绳子的质量和滑轮摩擦,则