题目内容
【题目】如图所示，在边长为2a的正三角形区域内存在方向垂直于纸面向里的匀强磁场，一个质量为m、电荷量为﹣q的带电粒子（重力不计）从AB边的中点O以速度v进入磁场，粒子进入磁场时的速度方向垂直于磁场且与AB边的夹角为60°，若要使粒子能从AC边穿出磁场，则匀强磁场的大小B需满足（ ）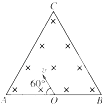
A.B＞ 
B.B＜
C.B＞ 
D.B＜
【答案】B
【解析】解：粒子刚好达到C点时，其运动轨迹与AC相切，如图所示：
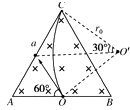
则粒子运动的半径为：r=acot30°= 
a，
洛伦兹力提供向心力，由牛顿第二定律得：
qvB=m 
，
解得：r= 
，
粒子要能从AC边射出，粒子运行的半径：R＞r，
解得：B＜ 
，
故选：B．
作出粒子在磁场中的运动轨迹，结合几何关系得到临界轨迹的轨道半径；再根据牛顿第二定律并结合洛伦兹力提供向心力列式求解．
练习册系列答案
相关题目
