题目内容
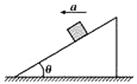
【题目】如图所示,质量m=1 kg的物块放在倾角θ=37°的斜面体上,要使物块与斜面体一起相对静止地沿水平方向向左做匀加速直线运动,则其加速度的取值范围是什么?已知物块与斜面体间的动摩擦因数μ=0.3,物块与斜面体间的最大静摩擦力可以认为等于它们间的滑动摩擦力,取重力加速度g=10 m/s2.
【答案】3.67 m/s2≤a≤13.5 m/s2
【解析】试题分析:对物体进行受力分析,由牛顿第二定律及平衡条件分别求出摩擦力向上和向下两种情况下的加速度,即可解题。
(1)当物体将要沿斜面向下滑时,设此时的加速度为a,其受力情况如图所示,
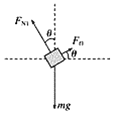
由牛顿第二定律有:![]()
由平衡条件有:![]()
又:![]()
联立以上并代入数据解得:a1≈3.67 m/s2
(2)当物体将要沿斜面向上滑动时,设此时的加速度为a2,其受力情况如图所示,
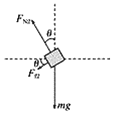
由牛顿第二定律有:![]()
由平衡条件有:![]()
又:![]()
联立以上并代入数据解得:a2≈13.5 m/s2
故要使物块与斜面体一起相对静止沿水平方向向左做加速直线运动,其加速度a应满足的条件为:3.67 m/s2≤a≤13.5 m/s2。

练习册系列答案
相关题目