题目内容
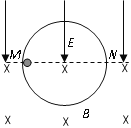
【题目】如图所示，有一位于竖直平面上的半径为R的圆形光滑绝缘轨道，其上半部分处于竖直向下、场强为
的匀强电场中，下半部分处于水平向里的匀强磁场中；质量为m，带正电为q的小球，从轨道的水平直径的M端由静止释放，若小球在某一次通过最低点时对轨道的压力为零，重力加速度为g，求：
（1）磁感强度B的大小；
（2）小球第二次通过轨道最低点时对轨道的压力；
（3）若小球恰好能在圆形轨道内做完整的圆周运动，则小球在轨道最高点的速度大小为多少？小球从M端出发时的竖直向下的速度大小是多少？
【答案】（1）
（2）6mg （3）
【解析】本题考查物体在复合场中的圆周运动
（1）小球在下半轨道上来回运动时受重力、支持力、洛仑兹力，但只有重力做功，因此小球的机械能守恒。从M到最低点有
在最低点有 
即
联解得
（2）小球从M到N以及在轨道上来回运动时受重力、支持力、洛仑兹力，但总只有重力做功，因此小球的机械能始终守恒。从N到最低点时对轨道最低点的有最大压力。
在最低点有 
解得N2=6mg
（3）要小球在圆形轨道内作完整的圆周运动，此时对圆形轨道的最高点压力为零，设小球从轨道的水平直径的M端下滑的最小速度为v0，在最高点速度为v1。
从M→轨道的最高点，据动能定理： 
在圆形轨道的最高点： 
解得
=
练习册系列答案
相关题目
