题目内容
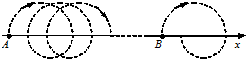 一质点在一平面内运动,其轨迹如图所示,它从A点出发,以恒定速率v0经时间t运动到B点.图中x轴上方的轨迹都是半径为R的半圆,下方都是半径为r的半圆.则此质点由A到B沿x轴运动的平均速度大小为
一质点在一平面内运动,其轨迹如图所示,它从A点出发,以恒定速率v0经时间t运动到B点.图中x轴上方的轨迹都是半径为R的半圆,下方都是半径为r的半圆.则此质点由A到B沿x轴运动的平均速度大小为分析:平均速度等于总位移除以总时间.
解答:解:设由A到B,若上、下各走了n个半圆,则运动的路程为s=nπ(R+r)
所以运动的时间为t=
=
其位移为:x=2n(R-r)
故其平均速度为
=
=
故答案案为:
所以运动的时间为t=
| s |
| v0 |
| nπ(R+r) |
| v0 |
其位移为:x=2n(R-r)
故其平均速度为
. |
| v |
| x |
| t |
| 2(R-r)v0 |
| π(R+r) |
故答案案为:
| 2(R-r)v0 |
| π(R+r) |
点评:本题主要考查了平均速度的定义,知道平均速度等于总位移除以总时间.

练习册系列答案
相关题目
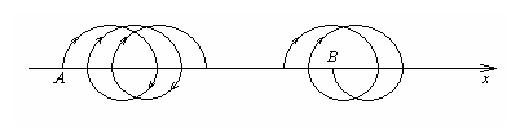
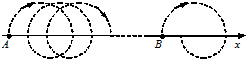 一质点在一平面内运动,其轨迹如图所示,它从A点出发,以恒定速率v0经时间t运动到B点.图中x轴上方的轨迹都是半径为R的半圆,下方都是半径为r的半圆.则此质点由A到B沿x轴运动的平均速度大小为________.
一质点在一平面内运动,其轨迹如图所示,它从A点出发,以恒定速率v0经时间t运动到B点.图中x轴上方的轨迹都是半径为R的半圆,下方都是半径为r的半圆.则此质点由A到B沿x轴运动的平均速度大小为________.