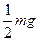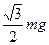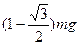题目内容
如图, 两绳系一个质量为m=0.1千克达到小球, 两绳的另两端分别固定于轴上的A、B两处, 上绳AC长L=2米, 两绳都拉直时与轴夹角分别是30°和45°,求小球的角速度在什么范围内取值, 两绳始终张紧?

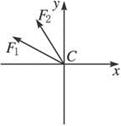
两绳张紧时,小球受的力如图所示,当ω由0逐渐增大时,ω可能出现两个临界值.
BC恰好拉直,但F2仍然为零,设此时的角速度为ω1,则有
Fx="F1sin30°=mω12Lsin30° " ① 2分
Fy="F1cos30°-mg=0 " ② 2分
代入已知解①②得 ω1="2.40" rad/s 1分
(2)AC由拉紧转为恰好拉直,但F1已为零,设此时的角速度为ω2,则有
Fx="F2sin45°=mω22Lsin30° " ③ 2分
Fy="F2cos45°-mg=0 " ④ 2分
代入已知解③④得 ω2="3.16" rad/s 1分
可见,要使两绳始终张紧,ω必须满足
2.40 rad/s<ω<3.16 rad/s. 2分
答案:2.40 rad/s<ω<3.16 rad/s

BC恰好拉直,但F2仍然为零,设此时的角速度为ω1,则有
Fx="F1sin30°=mω12Lsin30° " ① 2分
Fy="F1cos30°-mg=0 " ② 2分
代入已知解①②得 ω1="2.40" rad/s 1分
(2)AC由拉紧转为恰好拉直,但F1已为零,设此时的角速度为ω2,则有
Fx="F2sin45°=mω22Lsin30° " ③ 2分
Fy="F2cos45°-mg=0 " ④ 2分
代入已知解③④得 ω2="3.16" rad/s 1分
可见,要使两绳始终张紧,ω必须满足
2.40 rad/s<ω<3.16 rad/s. 2分
答案:2.40 rad/s<ω<3.16 rad/s
略

练习册系列答案
相关题目
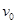 和位置s.
和位置s.

 通过转弯半径为
通过转弯半径为 的弯道时,内、外轨道均不受侧压力作用,下面分析正确的是
的弯道时,内、外轨道均不受侧压力作用,下面分析正确的是







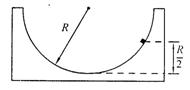
 的、半径为R的半圆形槽内,距最低点高为
的、半径为R的半圆形槽内,距最低点高为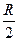 处,则它受到的摩擦力大小为 ( )
处,则它受到的摩擦力大小为 ( )