题目内容
1.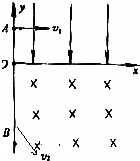 图中第I象限的区域里有平行于y轴的匀强电场E=2×104N/C,在第IV象限区域内有垂直于Oxy平面的匀强磁场B.带电粒子A,质量为m1=1×10-12kg,电量q1=1×10-4 C,从y轴上A点以平行于x轴的速度v1=4×105m/s射入电场中,已知OA=4×10-2m,
图中第I象限的区域里有平行于y轴的匀强电场E=2×104N/C,在第IV象限区域内有垂直于Oxy平面的匀强磁场B.带电粒子A,质量为m1=1×10-12kg,电量q1=1×10-4 C,从y轴上A点以平行于x轴的速度v1=4×105m/s射入电场中,已知OA=4×10-2m,(1)粒子A到达x轴的时间和位置.
(2)粒子A到达x轴的速度大小与方向.
(3)在粒子A射入电场的同时,粒子B从y轴上的某点B以与y轴负方向成45°角的速度v2射入匀强磁场中,A、B两个粒子恰好在x轴上迎面正碰(不计重力,也不考虑两个粒子间的库仑力)试确定B点的位置和B粒子在磁场中做圆周运动的周期T.
分析 (1)、(2)粒子垂直射入电场中做类平抛运动,根据类平抛运动的规律求解水平位移,确定粒子A到达x轴的位置和速度大小、方向.
(3)两个粒子要迎面正碰,速度方向相反,画出轨迹,确定出粒子在磁场中运动的时间,根据时间和周期的关系求解周期.
解答  解:(1)粒子A垂直射入电场中做类平抛运动,根据牛顿第二定律得:
解:(1)粒子A垂直射入电场中做类平抛运动,根据牛顿第二定律得:
加速度为 a=$\frac{{q}_{1}E}{{m}_{1}}$=$\frac{1×1{0}^{-4}×2×1{0}^{4}}{1×1{0}^{-12}}$m/s2=2×1012m/s2
由 $\overline{OA}$=$\frac{1}{2}a{t}^{2}$,得 t=$\sqrt{\frac{2\overline{OA}}{a}}$=$\sqrt{\frac{2×4×1{0}^{-2}}{2×1{0}^{-12}}}$s=2×10-7s
设粒子A通过x轴上的P点,则 $\overline{OP}$=v1t=4.0×105×2×10-7(m)=8×10-2m
(2)粒子到达P点的速度大小为 vP=$\sqrt{{v}_{1}^{2}+(at)^{2}}$=$\sqrt{(4×1{0}^{5})^{2}+(2×1{0}^{-12}×2×1{0}^{-7})^{2}}$m/s=4$\sqrt{2}$×105m/s
设vP与x轴正方向的夹角为α,则 cosα=$\frac{{v}_{1}}{{v}_{p}}$=$\sqrt{2}$,α=45°
(3)两个粒子要迎面正碰,画出轨迹如图所示.
根据几何关系可得 $\overline{OB}$=$\overline{OP}$=8×10-2m,则B点的位置坐标为(0,-8×10-2m)
由题设条件得知,粒子M在磁场中运动的时间也为 t=2×10-7s
且有 $\frac{t}{2}$=T
故B粒子在磁场中做圆周运动的周期 T=2t=4×10-7s
答:(1)粒子A到达x轴的时间为2×10-7s,位置坐标为(8×10-2m,0).
(2)粒子A到达x轴的速度大小为4$\sqrt{2}$×105m/s,方向与x轴正方向成45°角斜向右下方.
(3)B点的位置坐标为(0,-8×10-2m),B粒子在磁场中做圆周运动的周期是4×10-7s.
点评 本题是带电粒子在组合场中运动的类型,画出磁场中运动轨迹,电场中运用运动的分解都是常规方法,要能灵活运用几何知识求解磁场中空间尺寸.

 一定质量的理想气体状态变化过程如图所示,第1种变化是从A到B,第2种变化是从A到C,比较两种变化过程( )
一定质量的理想气体状态变化过程如图所示,第1种变化是从A到B,第2种变化是从A到C,比较两种变化过程( )| A. | 两个过程气体吸收热量一样 | B. | 两个过程气体内能增加不相同 | ||
| C. | A到C过程气体吸收热量较多 | D. | A到B过程气体吸收热量较多 |
| A. | 磁感线和电场线一定是封闭的曲线 | |
| B. | 磁感线和电场线是人们为了研究问题的方便而假想的曲线 | |
| C. | 磁感线是从N极出发到S极终止,电场线是从正电荷出发到负电荷终止 | |
| D. | 磁感线是磁场中铁屑排列成的曲线,而电场线是点电荷在电场中运动的轨迹 |
 如图所示,斜劈A静止放在水平地面上,木桩B固定在水平地面上,弹簧把物体与木桩相连且平行于斜面.物体m、人和A均保持静止.不计m与A之间的摩擦,则下列说法正确的是( )
如图所示,斜劈A静止放在水平地面上,木桩B固定在水平地面上,弹簧把物体与木桩相连且平行于斜面.物体m、人和A均保持静止.不计m与A之间的摩擦,则下列说法正确的是( )| A. | 地面对A的摩擦力向左 | |
| B. | 若剪断弹簧,物体和人将向下运动,而A仍保持静止 | |
| C. | 若人从物体m离开,物体m仍静止在斜劈A上 | |
| D. | 若剪断弹簧同时人从物体m离开,地面对A的摩擦力为零 |
| A. | 若车加速前进,马拉车的力小于车拉马的力 | |
| B. | 若车加速前进,马拉车的力大于车拉马的力 | |
| C. | 只有车匀速前进,马拉车的力才与车拉马的力相等 | |
| D. | 不论车如何运动,马拉车的力和车拉马的力总是大小相等的 |
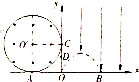 如图所示的xOy平面,在第二象限有一半径为R的匀强磁场区域,圆心为O′(-R,R),磁场方向垂直xOy平面向外,磁感应强度为B.在第一象限的虚线上方存在一沿y轴负方向的匀强电场,虚线为电场的边界,其方程为y=$\frac{8}{3R}$x(R-x).在A点有一粒子源,能不断向x轴上方各个方向均匀发射质量为m,电荷量为q(q>0)的同种带电粒子,所有粒子发射速率相同.已知沿y轴正方向入射的粒子通过C点(0,R)后,沿与x轴正方形成53°角方向斜向下打到B点,B、D点坐标分别为(R,0),(O,$\frac{R}{2}$),不计粒子间的相互作用和重力.sin53°=0.8,cos53°=0.6.求:
如图所示的xOy平面,在第二象限有一半径为R的匀强磁场区域,圆心为O′(-R,R),磁场方向垂直xOy平面向外,磁感应强度为B.在第一象限的虚线上方存在一沿y轴负方向的匀强电场,虚线为电场的边界,其方程为y=$\frac{8}{3R}$x(R-x).在A点有一粒子源,能不断向x轴上方各个方向均匀发射质量为m,电荷量为q(q>0)的同种带电粒子,所有粒子发射速率相同.已知沿y轴正方向入射的粒子通过C点(0,R)后,沿与x轴正方形成53°角方向斜向下打到B点,B、D点坐标分别为(R,0),(O,$\frac{R}{2}$),不计粒子间的相互作用和重力.sin53°=0.8,cos53°=0.6.求: 如图所示.电荷均匀分布在带电圆环上.圆环总电荷量为=Q.在圆环的轴上与圆环圆心O距离L处放有一点电荷+q,已知圆环半径为R.此时圆环对点电荷+q的作用力大小为多少?方向怎样?
如图所示.电荷均匀分布在带电圆环上.圆环总电荷量为=Q.在圆环的轴上与圆环圆心O距离L处放有一点电荷+q,已知圆环半径为R.此时圆环对点电荷+q的作用力大小为多少?方向怎样? 如图所示,在x轴的上方有磁感应强度为B的匀强磁场,方向垂直纸面向里.在x轴的下方有电场强度为E的匀强电场,方向与y轴负方向成θ角.一个带电量为+q、质量为m的粒子以初速度v0从A点进入磁场.v0方向与磁场方向垂直,与y轴正方向成θ角.粒子从x轴射出磁场的速度恰与射入磁场时的速度反向(即与电场方向相同);不计重力.求:
如图所示,在x轴的上方有磁感应强度为B的匀强磁场,方向垂直纸面向里.在x轴的下方有电场强度为E的匀强电场,方向与y轴负方向成θ角.一个带电量为+q、质量为m的粒子以初速度v0从A点进入磁场.v0方向与磁场方向垂直,与y轴正方向成θ角.粒子从x轴射出磁场的速度恰与射入磁场时的速度反向(即与电场方向相同);不计重力.求: