题目内容
（2008?杭州一模）如图所示，在一粗糙水平上有两个质量分别为m1和m2的木块1和2，中间用一原长为l、劲度系数为k的轻弹簧连接起来，木块与地面间的动摩擦因数为μ，现用一水平力向左拉木块1，当两木块一起匀速运动时两木块之间的距离是（ ）分析：当两木块一起匀速运动时，木块2受到重力、弹簧的拉力、地面的支持力和摩擦力而平衡，根据平衡条件求出弹簧的弹力，由胡克定律求出弹簧伸长的长度，再求解两木块之间的距离．
解答：解：对木块2受力分析如图：
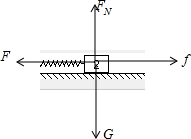
根据平衡条件弹簧的弹力F=μm2g
又由胡克定律：F=kx
整理：x=
=
所以弹簧的长度为：l+x=l+
故选：C
根据平衡条件弹簧的弹力F=μm2g
又由胡克定律：F=kx
整理：x=
| F |
| k |
| μm2g |
| k |
所以弹簧的长度为：l+x=l+
| μm2g |
| k |
故选：C
点评：本题是平衡条件和胡克定律的综合应用，关键是选择研究对象，分析物体的受力情况．
练习册系列答案
相关题目
（2008?杭州一模）某同学用如图所示的电路进行小电机M的输出功率的研究，其实验步骤如下所述，闭合电键后，调节滑动变阻器，电动机未转动时，电压表的读数为U1，电流表的读数为I1；再调节滑动变阻器，电动机转动后电压表的读数为U2，电流表的读数为I2，则此时电动机的输出功率为（ ）
（2008?杭州一模）水平拉力F1、F2分别作用在水平面的物体上一段时间后又撤去，使物体都由静止开始运动而后又停下．如果物体在两种情况下的总位移相等，且F1＞F2，那么在这样的情况中（ ）