题目内容
如图1所示,绝缘水平面上相距L=1.6m的空间内存在水平向左的匀强电场E,质量m=O.1kg、带电量q=+1xl0-7 C的滑块(视为质点)以V0=4m/s的初速度沿水平面向右进入电场区域,滑块与水平面间的动摩擦因数μ=0.4,设是大静摩擦力与滑动摩擦力相等.(g取1Om/s2)
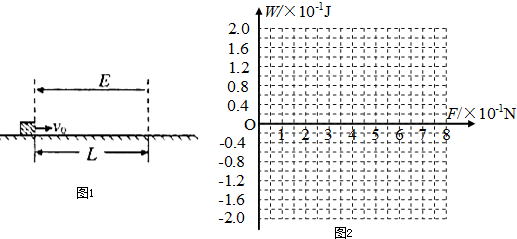
(1)如果滑块不能离开电场区域,电场强度E的取值范围多大
(2)如果滑块能离开电场区域,试在图2W-F坐标中画出电场力对滑块所做的功W与电场力F的关系图象.

(1)如果滑块不能离开电场区域,电场强度E的取值范围多大
(2)如果滑块能离开电场区域,试在图2W-F坐标中画出电场力对滑块所做的功W与电场力F的关系图象.
分析:(1)要使下滑块不从右侧离开磁场区域,根据牛顿第二定律求出匀减速直线运动的加速度,抓住临界情况,到达右侧速度为零,求出电场强度的最小值.若小滑块不从左侧滑出,则速度减为零后,不再运动,即电场力小于最大静摩擦力,从而求出电场强度的最大值.
(2)若电场强度小于最小值,则能从右侧离开电场,通过位移求出电场力做功与电场力的关系.若电场强度大于最大值,则滑块从左侧离开电场,此时电场力做功为零.作出W与F的关系图线.
(2)若电场强度小于最小值,则能从右侧离开电场,通过位移求出电场力做功与电场力的关系.若电场强度大于最大值,则滑块从左侧离开电场,此时电场力做功为零.作出W与F的关系图线.
解答:解:(1)小滑块在摩擦力和电场力作用下,向右做匀减速运动,设加速度为a,根据牛顿第二定律得:
F+f=ma…①
又F=qE…②
f=μmg…③
若小滑块不会从右侧离开电场区域,由匀变速直线运动的规律有:
v02<2aL…④
联立①②③④,并代入数据得:E>106N/C…⑤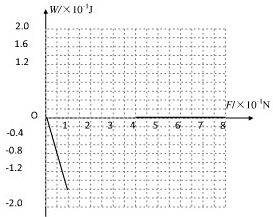
若小滑块不会从左侧离开电场区域,必须满足:F≤f…⑥
由②⑤⑥可得:106N/C<E≤4×106N/C…⑦
(2)小滑块不离开电场时,最小电场力F=qE=1.0×10-7×106N=0.1N
最大电场力F=qE=1×10-7×4×106N=0.4N
若F≤0.1N,小滑块将从右侧离开电场区域,此过程小滑块的电场中的位移s=1.6m,则电场力做功W=-Fs=-1.6F.
若F>0.4N,小滑块将从右侧离开电场区域,此过程中小滑块在电场中的位移s=0,电场力做功为0,则W=0.
答:(1)如果滑块不能离开电场区域,电场强度E的取值范围106N/C<E≤4×106N/C.
(2)如图所示.
F+f=ma…①
又F=qE…②
f=μmg…③
若小滑块不会从右侧离开电场区域,由匀变速直线运动的规律有:
v02<2aL…④
联立①②③④,并代入数据得:E>106N/C…⑤

若小滑块不会从左侧离开电场区域,必须满足:F≤f…⑥
由②⑤⑥可得:106N/C<E≤4×106N/C…⑦
(2)小滑块不离开电场时,最小电场力F=qE=1.0×10-7×106N=0.1N
最大电场力F=qE=1×10-7×4×106N=0.4N
若F≤0.1N,小滑块将从右侧离开电场区域,此过程小滑块的电场中的位移s=1.6m,则电场力做功W=-Fs=-1.6F.
若F>0.4N,小滑块将从右侧离开电场区域,此过程中小滑块在电场中的位移s=0,电场力做功为0,则W=0.
答:(1)如果滑块不能离开电场区域,电场强度E的取值范围106N/C<E≤4×106N/C.
(2)如图所示.
点评:本题综合考查了牛顿第二定律和运动学公式的运用,滑块不能出电场,需讨论不能从右侧和左侧出电场.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目