题目内容
 如图所示,以坐标原点O为圆心的半径为R的半圆形区域里,有一垂直纸面向里的匀强磁场(包括边界),磁感应强度为B.图中abcd是一个外切于半圆的矩形边界线.在-R≤y≤R的区间内,有一束速度相同的带电粒子垂直y轴射入磁场区域,粒子的质量为m、电荷量为q,粒子的重力忽略不计.结果检测到矩形边界线的ab、be段均有粒子射出,而矩形边界线其余部分均无粒子射出.求:
如图所示,以坐标原点O为圆心的半径为R的半圆形区域里,有一垂直纸面向里的匀强磁场(包括边界),磁感应强度为B.图中abcd是一个外切于半圆的矩形边界线.在-R≤y≤R的区间内,有一束速度相同的带电粒子垂直y轴射入磁场区域,粒子的质量为m、电荷量为q,粒子的重力忽略不计.结果检测到矩形边界线的ab、be段均有粒子射出,而矩形边界线其余部分均无粒子射出.求:(1)粒子入射的速度是多大?
(2)从O点入射的粒子,从矩形边界线上的什么位置射出.
(3)从(0,
| R | 2 |
分析:因为在ab、be段均有粒子射出,其余部分均无粒子射出,所以粒子带正电,且粒子在磁场中的轨迹半径满足r=R,根据洛伦兹力提供向心力列式,可求得入射速度
做出粒子运动轨迹图,根据几何关系求解坐标
做出粒子运动轨迹图,根据几何关系求解坐标
解答:解:(1)因为在ab、be段均有粒子射出,其余部分均无粒子射出,所以粒子带正电,且粒子在磁场中的轨迹半径满足:r=R
又根据 qvB=m
得入射粒子的速度 v=
(2)从O点入射的粒子,从E点射出磁场,经过边界线be上的D点,如图甲所示.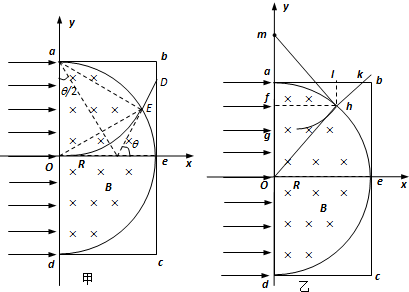
因为OE孤的半径r=R,
所以OE孤的圆心即为a点,△aOE为等边三角形,θ=60°,则D点的坐标值:xD=R
yD=(R-Rtan
)?tanθ=(
-1)R
(3)从y=
的g点射入,在h点射出磁场,
在k点射出矩形边界线,如图乙所示
=
=
R
=
=
=
=
R
=
=
-
=R-
R=
R
△m f h 相似于△klh
=
即:
=
=
则k点的位置坐标:xk=
+
=
R+
R=
R
yk=R
答:(1)粒子入射的速度
(2)从O点入射的粒子,从矩形边界线上的(R,(
-1)R)位置射出.
(3)从(0,
)点入射的粒子,从矩形边界线上的(
R,R)位置射出.
又根据 qvB=m
| v2 |
| r |
得入射粒子的速度 v=
| qBR |
| m |
(2)从O点入射的粒子,从E点射出磁场,经过边界线be上的D点,如图甲所示.

因为OE孤的半径r=R,
所以OE孤的圆心即为a点,△aOE为等边三角形,θ=60°,则D点的坐标值:xD=R
yD=(R-Rtan
| θ |
| 2 |
| 3 |
(3)从y=
| R |
| 2 |
在k点射出矩形边界线,如图乙所示
. |
| mf |
R+
| ||
| 2 |
| 3 |
| 4 |
. |
| al |
. |
| fh |
R2-
|
R2-(
|
| ||
| 4 |
. |
| lh |
. |
| af |
. |
| oa |
. |
| of |
| 3 |
| 4 |
| 1 |
| 4 |
△m f h 相似于△klh
| ||
|
| ||
|
即:
| ||
|
| ||||
|
. |
| lk |
3
| ||
| 28 |
则k点的位置坐标:xk=
. |
| al |
. |
| lk |
| ||
| 4 |
3
| ||
| 28 |
5
| ||
| 14 |
yk=R
答:(1)粒子入射的速度
| qBR |
| m |
(2)从O点入射的粒子,从矩形边界线上的(R,(
| 3 |
(3)从(0,
| R |
| 2 |
5
| ||
| 14 |
点评:本题考查粒子在磁场中的运动,洛伦兹力提供向心力,做出粒子的运动轨迹图是关键.

练习册系列答案
相关题目
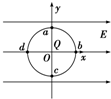 如图所示,以坐标原点O为圆心,半径为r的圆与坐标轴交于a、b、c、d.在O点固定一个正点电荷Q,另有一沿x轴正方向,场强大小为E的匀强电场,当点电荷+q在电场中移动时( )
如图所示,以坐标原点O为圆心,半径为r的圆与坐标轴交于a、b、c、d.在O点固定一个正点电荷Q,另有一沿x轴正方向,场强大小为E的匀强电场,当点电荷+q在电场中移动时( )| A、从a移到b,电场力不做功 | B、从a移到c,电场力不做功 | C、从d移到b,电场力做功为2qEr | D、从d移到a,电场力做功为2qEr |


