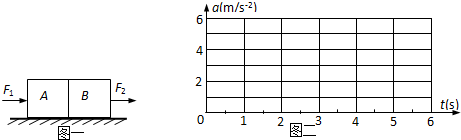题目内容
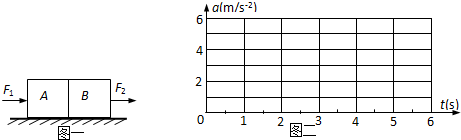
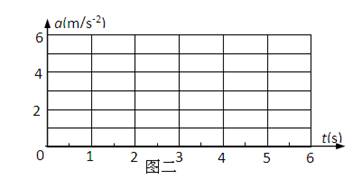
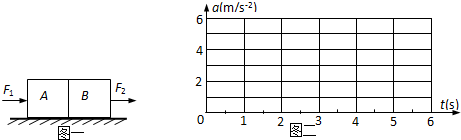
如图一所示，质量分别为m1=1kg和m2=2kg的A、B两物块并排放在光滑水平面上，若对A、B分别施加大小随时间变化的水平外力F1和F2，其中F1=（9-2t）N，F2=（3+2t）N，请回答下列问题：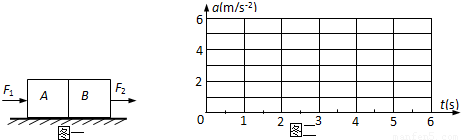
（1）A、B两物块在未分离前的加速度是多大？
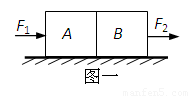
（2）通过计算在图二坐标系中画出两物块的加速度随时间变化的图象．
（3）求出A、B两物块自分离后，经过2s时的速度大小之差．
【答案】分析：（1）A、B两物块在未分离前加速度相同，根据牛顿第二定律求解加速度．
（2）由牛顿第二定律分别求出两个物块的加速度，作出图象；
（3）加速度的定义为a=△v/△t，则“a-t”图象下的“面积”在数值上应等于速度的变化量△v，图象所围三角形的面积即为分离后2s时的速度大小之差．
解答：解：：（1）对A、B整体，由牛顿第二定律得：
F1+F2=（m1+m2）a
故a=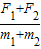
=
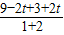m/s2=4m/s2
（2）当A、B间的弹力为0时，A、B分离，刚分离时：
=
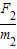
即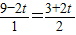
可求出t=2.5s
即t=0-2.5s内A和B的加速度恒为4m/s2
A、B分离后，
对A：a1=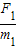
=
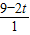m/s2=（9-2t）m/s2，图象如图所示
对B：a2=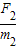
=
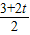m/s2=（1.5+t）m/s2，图象如图所示
（3）如图图中阴影部分三角形面积表示两物块的速度差即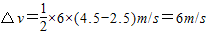
答：（1）A、B两物块在未分离前的加速度是4m/s2；
（2）通过计算在图二坐标系中画出两物块的加速度随时间变化的图象如图所示；
（3）A、B两物块自分离后，经过2s时的速度大小之差为△v=6m/s．
点评：本题是连接体问题，采用整体法和隔离法相结合的处理方法，刚分离时的临界条件是两物体间的弹力等于零，是常用的临界条件．
（2）由牛顿第二定律分别求出两个物块的加速度，作出图象；
（3）加速度的定义为a=△v/△t，则“a-t”图象下的“面积”在数值上应等于速度的变化量△v，图象所围三角形的面积即为分离后2s时的速度大小之差．
解答：解：：（1）对A、B整体，由牛顿第二定律得：
F1+F2=（m1+m2）a
故a=
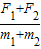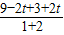=m/s2=4m/s2（2）当A、B间的弹力为0时，A、B分离，刚分离时：
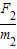
=即
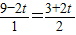
可求出t=2.5s
即t=0-2.5s内A和B的加速度恒为4m/s2
A、B分离后，
对A：a1=
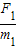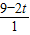=m/s2=（9-2t）m/s2，图象如图所示对B：a2=
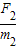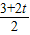=m/s2=（1.5+t）m/s2，图象如图所示（3）如图图中阴影部分三角形面积表示两物块的速度差即
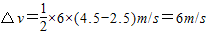
答：（1）A、B两物块在未分离前的加速度是4m/s2；
（2）通过计算在图二坐标系中画出两物块的加速度随时间变化的图象如图所示；
（3）A、B两物块自分离后，经过2s时的速度大小之差为△v=6m/s．
点评：本题是连接体问题，采用整体法和隔离法相结合的处理方法，刚分离时的临界条件是两物体间的弹力等于零，是常用的临界条件．
练习册系列答案
相关题目
