题目内容
两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面,如图所示.现将质量相同的两个小球,分别从两个碗的边缘处由静止释放(小球半径远小于碗的半径),两个小球通过碗的最低点时( )
A.两小球速度大小不等,对碗底的压力相等
B.两小球速度大小不等,对碗底的压力不等
C.两小球速度大小相等,对碗底的压力相等
D.两小球速度大小相等,对碗底的压力不等
【答案】分析:根据动能定理研究小球从碗的边缘到碗的最低点,列出等式求出两小球速度大小关系.
对小球在碗的最低点进行受力分析,找出向心力的来源,根据牛顿第二定律表示出碗对球的支持力.
解答:解:设大碗的半径为r1,设小碗的半径为r2,
根据动能定理研究小球从碗的边缘到碗的最低点,列出等式得:
mgr1= mv12-0,得:v1=
mv12-0,得:v1=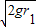
mgr2= mv22-0 得:v2=
mv22-0 得:v2=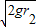
由于r1>r2,所以v1>v2
对小球在碗的最低点进行受力分析,小球受重力和碗对球的支持力FN,根据牛顿第二定律得:
F合=FN-mg=ma
向心加速度a=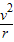
FN=mg+m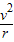
FN1=mg+m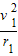 =3mg
=3mg
FN2=mg+m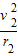 =3mg
=3mg
所以FN1=FN2
根据牛顿第三定律知道碗对球的支持力等于球对压力
故选A.
点评:选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.
要去比较一个物理量两种情况下的大小关系,我们应该通过物理规律先把这个物理量表示出来.
对小球在碗的最低点进行受力分析,找出向心力的来源,根据牛顿第二定律表示出碗对球的支持力.
解答:解:设大碗的半径为r1,设小碗的半径为r2,
根据动能定理研究小球从碗的边缘到碗的最低点,列出等式得:
mgr1=
 mv12-0,得:v1=
mv12-0,得:v1=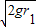
mgr2=
 mv22-0 得:v2=
mv22-0 得:v2=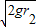
由于r1>r2,所以v1>v2
对小球在碗的最低点进行受力分析,小球受重力和碗对球的支持力FN,根据牛顿第二定律得:
F合=FN-mg=ma
向心加速度a=
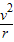
FN=mg+m
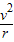
FN1=mg+m
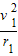 =3mg
=3mgFN2=mg+m
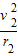 =3mg
=3mg所以FN1=FN2
根据牛顿第三定律知道碗对球的支持力等于球对压力
故选A.
点评:选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.
要去比较一个物理量两种情况下的大小关系,我们应该通过物理规律先把这个物理量表示出来.

练习册系列答案
相关题目
 如图所示,两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面.将质量相同的两小球(小球半径远小于碗的半径)分别从两个碗的边缘由静止释放,当两球分别通过碗的最低点时( )
如图所示,两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面.将质量相同的两小球(小球半径远小于碗的半径)分别从两个碗的边缘由静止释放,当两球分别通过碗的最低点时( )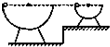 如图所示,两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面(设为零势能面),现将质量相同的两个小球(小球半径远小于碗的半径)分别从两个碗的边缘由静止释放,当两球分别通过碗的最低点时( )
如图所示,两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面(设为零势能面),现将质量相同的两个小球(小球半径远小于碗的半径)分别从两个碗的边缘由静止释放,当两球分别通过碗的最低点时( )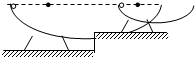 如图所示两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面.现将质量相同的两个小球(小球半径远小于碗的半径),分别从两个碗的边缘由静止释放(忽略空气阻力),则( )
如图所示两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面.现将质量相同的两个小球(小球半径远小于碗的半径),分别从两个碗的边缘由静止释放(忽略空气阻力),则( )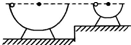 如图为两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面.现将质量相同的两个带等量负电荷的小球(小球半径远小于碗的半径)分别从两个碗的边缘由静止释放,当两小球分别沿圆弧通过碗的最低点时,下列说法正确的有( )
如图为两个内壁光滑、半径不同的半球形碗,放在不同高度的水平面上,使两碗口处于同一水平面.现将质量相同的两个带等量负电荷的小球(小球半径远小于碗的半径)分别从两个碗的边缘由静止释放,当两小球分别沿圆弧通过碗的最低点时,下列说法正确的有( )