题目内容

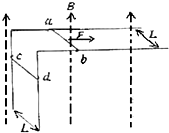
如图所示，MN、PQ是与水平面成θ角的两条平行光滑且足够长的金属导轨，其电阻忽略不计．空间存在着垂直于轨道平面向上的匀强磁场，磁感应强度大小为B．导体棒ab、cd垂直于导轨放置，且与轨道接触良好，每根导体棒的质量均为m，电阻均为r，轨道宽度为L．与导轨平行的绝缘细线一端固定，另一端与ab棒中点连接，细线承受的最大拉力Tm=2mgsinθ．今将cd棒由静止释放，则细线被拉断时，cd棒的（　　）
A．速度大小是
2mgrsinθ
B2L2
B．速度大小是
mgrsinθ
B2L2
C．加速度大小是2gsinθ
D．加速度大小是0

AB、据题知，细线被拉断时，拉力达到Tm=2mgsinθ．
根据平衡条件得：对ab棒：Tm=F安+mgsinθ．则得ab棒所受的安培力大小为F安=mgsinθ；
由于两棒的电流相等，所受的安培力大小相等．
由E=BLv、I=
E
2r
，F安=BIL，则得F安=
B2L2v
2r

联立解得，cd棒的速度为 v=
2mgrsinθ
B2L2
．故A正确，B错误．
CD、对cd棒：根据牛顿第二定律得：mgsinθ-F安=ma，代入得a=gsinθ-
1
m
?
B2L2
2r
?
2mgrsinθ
B2L2
=0，故C错误，D正确．
故选：AD．
练习册系列答案
相关题目
如图所示，平行光滑导轨OPQ、OˊPˊQˊ相距L=0.5m，导轨平面与水平面成θ=53°角，OP段和OˊPˊ段是导电的，PQ段和PˊQˊ段是绝缘的，在P和Pˊ处固定一个“∩”形导体框abcd，导体框平面与导轨面垂直，面积S=0.3m2．空间存在变化的匀强磁场，方向与导轨平行，与线圈abcd垂直．质量为m=0.02kg、电阻R=0.2Ω的金属棒AB放在两导轨上QQˊ处，与PPˊ的距离x=0.64m，棒与导轨垂直并保持良好接触．t=0时刻，从QQˊ无初速度释放金属棒AB，此时匀强磁场方向沿导轨向上（规定为正方向），磁感应强度B的变化规律为B=0.2-0.8t（T）．除金属棒AB外，不计其它电阻．求：
（1）经过多长时间，金属棒AB中有感应电流？感应电流的方向如何？
（2）假设OP段和OˊPˊ段的导轨足够长，金属棒AB在OP段和OˊPˊ段的导轨上能滑行多远？
（sin53°=0.8，cos53°=0.6，g取10m/s2）
一个边长为a=1m的正方形线圈，总电阻为R=2Ω，当线圈以v=2m/s的速度通过磁感应强度为B=0.5T的匀强磁场区域时，线圈平面总保持与磁场垂直．若磁场的宽度b＞1m，如图所示，求：
（1）线圈进入磁场过程中感应电流的大小；
（2）线圈在穿过整个磁场过程中释放的焦耳热．
如图所示，单匝线圈ABCD在外力作用下以速度V向右匀速进入匀强磁场，第二次又以速度2V匀速进入同一匀强磁场．则下说法说正确的是（　　）
A．第二次与第一次通过AB边横截面的电荷量之比为2：1
B．第二次与第一次线圈中产生的热量之比为4：1
C．第二次与第一次线圈中最大电流之比为2：1
如图所示，两根相距为L的足够长的金属直角导轨如图所示放置，它们各有一边在同一水平面内，另一边垂直于水平面．质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路，杆与导轨之间的动摩擦因数均为μ，导轨电阻不计，回路总电阻为2R．整个装置处于磁感应强度大小为B，方向竖直向上的匀强磁场中．当ab杆在平行于水平导轨的拉力F作用下以速度V1沿导轨匀速运动时，cd杆也正好以速度V2向下匀速运动．重力加速度为g．以下说法正确的是（　　）
A．ab杆所受拉力F的大小为μmg+
B2L2V1
2R
B．cd杆所受摩擦力为零
C．回路中的电流强度为BL
(V1+V2)
2R
D．μ与V1大小的关系为μ=
2mgR
B2L2v1
如图所示，两根完全相同的“V”字形导轨OPQ与KMN倒放在绝缘水平面上，两导轨都在竖直平面内且正对、平行放置，其间距为L，电阻不计．两条导轨足够长，所形成的两个斜面与水平面的夹角都是α．两个金属棒ab和a′b′的质量都是m，电阻都是R，与导轨垂直放置且接触良好．空间有竖直向下的匀强磁场，磁感应强度为B．
（1）如果两条导轨皆光滑，让a′b′固定不动，将ab释放，则ab达到的最大速度是多少？
（2）如果将ab与a′b′同时释放，它们所能达到的最大速度分别是多少？
如图甲所示，空间存在一宽度为2L有界匀强磁场，磁场方向垂直纸面向里．在光滑绝缘水平面内有一边长为L的正方形金属线框，其质量m=1kg、电阻R=4Ω，在水平向左的外力F作用下，以初速度v0=4m/s匀减速进入磁场，线框平面与磁场垂直，外力F大小随时间t变化的图线如图乙所示．以线框右边刚进入磁场时开始计时，求：
（1）匀强磁场的磁感应强度B；
（2）线框进入磁场的过程中，通过线框的电荷量q；
（3）判断线框能否从右侧离开磁场？说明理由．
如图所示，足够长的光滑平行金属导轨MN、PQ竖直放置，导轨间距为L=0.40m，一个磁感应强度B=0.50T的匀强磁场垂直穿过导轨平面，导轨的上端M与P间接有阻值为R=0.30Ω的电阻，一电阻为r=0.20Ω的金属棒ab紧贴在导轨上．现使金属棒ab由静止开始下滑，通过传感器记录金属棒ab在不同时刻的位置（如下表），导轨电阻不计，重力加速度g=10m/s2．求：
时刻t/s00.100.200.300.400.500.600.70
位置x/m00.100.300.701.201.702.202.70
（1）在前0.4s的时间内，金属棒ab电动势的平均值
.
E
；
（2）金属棒的质量m；
（3）在前0.7s的时间内，回路产生的焦耳热Q．
如图，足够长平行金属导轨内有垂直纸面向里的匀强磁场，金属杆ab与导轨垂直且接触良好，导轨右端通过电阻与平行金属板AB连接．已知导轨相距为L；磁场磁感应强度为B；R1、R2和ab杆的电阻值均为r，其余电阻不计；板间距为d、板长为4d；重力加速度为g，不计空气阻力．
如果ab杆以某一速度向左匀速运动时，沿两板中心线水平射入质量为m、带电量为+q的微粒恰能沿两板中心线射出；如果ab杆以同样大小的速度向右匀速运动时，该微粒将射到B板距左端为d的C处．
（1）求ab杆匀速运动的速度大小v；
（2）求微粒水平射入两板时的速度大小v0；
（3）如果以v0沿中心线射入的上述微粒能够从两板间射出，试讨论ab杆向左匀速运动的速度范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网