题目内容
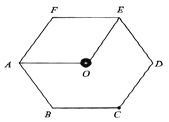
【题目】如图所示,处于竖直平面内的正六边形金属框架ABCDEF、可绕过C点且与平面垂直的水平轴自由转动,该金属框架的边长为L,中心记为O,用两根不可伸长、长度均为L的轻质细线将质量为m的金属小球悬挂于框架的A、E两个顶点并处于静止状态,现令框架绕转轴、沿顺时针方向缓慢转过90°角,已知重力加速度为g,在包括初、末状态的整个转动过程中下列说法正确的是( )
A. 细线OA中拉力最大值为mg
B. 细线OE中拉力最大值为![]()
C. 细线OA中拉力逐渐增大
D. 细线OE中拉力逐渐减小
【答案】BD
【解析】对小球进行受力分析,如图所示,

Mg的对角始终为1200,设FTA的对角为![]() ,FTE的对角为
,FTE的对角为![]() ,缓慢转动过程中,小球始终受力平衡,由正弦定理得
,缓慢转动过程中,小球始终受力平衡,由正弦定理得![]() ,
, ![]() 角由1500减小到600,FTA先增大后减小,当
角由1500减小到600,FTA先增大后减小,当![]() 时,FTA最大,最大值为
时,FTA最大,最大值为![]() ,故A、C错误;
,故A、C错误;
![]() 角由900增加到1800,FTE减小到0,当
角由900增加到1800,FTE减小到0,当![]() 时,FTE最大,最大值为
时,FTE最大,最大值为![]() ,故B、D正确。
,故B、D正确。
点晴:解决本题关键正确的受力分析,判断出角度的变化,由正弦定理求解。

练习册系列答案
相关题目