题目内容
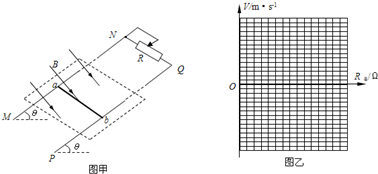如图甲所示，两根光滑的金属导轨MN、PQ彼此平行，相距L=0.5m，与水平面成θ=37°角放置，在导轨的上部接有一滑动变阻器，其最大阻值R=10Ω．一根质量为m=50g、电阻r=2Ω的直导体棒ab与导轨垂直放置且与导轨接触良好．在图示的矩形虚线区域内存在着垂直导轨平面向下、磁感应强度B=2T的匀强磁场，该磁场始终以速度v0在矩形虚线区域内沿着导轨匀速向上运动．当滑片滑至滑动变阻器的中点时，导体棒恰能在导轨上静止不动．金属导轨的电阻不计，运动的过程中总能保证金属棒处于磁场中．设轨道足够长，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8．（1）求磁场运动的速度v0是多大？
（2）现将滑动变阻器接入电路的阻值迅速变为1Ω，求导体棒稳定运动时的速度大小及该过程中安培力的最大功率．
（3）若将滑动变阻器的滑片滑至某处后导体棒稳定运动时的速度用符号v表示，此时对应电路的总电阻用符号R总表示，请推导速度v随总电阻R总变化的关系式，并在图乙中准确地画出此情况下的v-R总图象．
分析：（1）根据导体棒处于平衡，根据共点力平衡，结合闭合电路欧姆定律和切割产生的感应电动势求出磁场的运动的速度．
（2）根据导体棒稳定时，处于平衡求出导体棒相对于磁场的速度大小，从而求出导体棒稳定时的速度大小．当相对于磁场速度最大时，产生的电功率最大．
（3）根据稳定时平衡推导出相对速度与总电阻的关系式，从而推导出速度v随总电阻R总变化的关系式．
（2）根据导体棒稳定时，处于平衡求出导体棒相对于磁场的速度大小，从而求出导体棒稳定时的速度大小．当相对于磁场速度最大时，产生的电功率最大．
（3）根据稳定时平衡推导出相对速度与总电阻的关系式，从而推导出速度v随总电阻R总变化的关系式．
解答：解：（1）根据BIL=mgsin37°
又I=
联立解得：v0=
=2.1m/s．
（2）当导体棒稳定时，有：mgsin37°=
代入数据解得，v相对=0.9m/s，
则导体棒的速度v=v0-v相对=2.1-0.9=1.2m/s．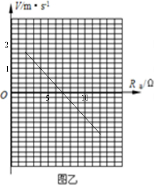
当金属棒相对磁场速度与2.1m/s时，产生的感应电流最大，安培力的功率最大，
有Pm=
=
W=1.47W．
（3）根据mgsin37°=
解得v相对=
=0.3R总
则v=v0-v相对=2.1-0.3R总（2Ω≤R总≤12Ω）．
答：（1）磁场运动的速度v0是2.1m/s．
（2）导体棒稳定运动时的速度大小为1.2m/s，安培力最大功率为1.47W．
（3）速度v随总电阻R总变化的关系式为2.1-0.3R总（2Ω≤R总≤12Ω）．
又I=
| BLv0 |
| R+r |
联立解得：v0=
| mg(R+r) |
| B2L2 |
（2）当导体棒稳定时，有：mgsin37°=
| B2L2v相对 |
| R′+r |
代入数据解得，v相对=0.9m/s，
则导体棒的速度v=v0-v相对=2.1-0.9=1.2m/s．
当金属棒相对磁场速度与2.1m/s时，产生的感应电流最大，安培力的功率最大，
有Pm=
| B2L2vm2 |
| R′+r |
4×
| ||
| 3 |
（3）根据mgsin37°=
| B2L2v相对 |
| R总 |
解得v相对=
| mgR总sin37° |
| B2L2 |
则v=v0-v相对=2.1-0.3R总（2Ω≤R总≤12Ω）．
答：（1）磁场运动的速度v0是2.1m/s．
（2）导体棒稳定运动时的速度大小为1.2m/s，安培力最大功率为1.47W．
（3）速度v随总电阻R总变化的关系式为2.1-0.3R总（2Ω≤R总≤12Ω）．
点评：解决本题的关键确定导体棒相对于磁场的速度，抓住受到重力的分力和安培力平衡进行求解．
练习册系列答案
相关题目
如图甲所示，两根足够长的平行光滑金属导轨固定放置在水平面上，间距L=0.2m，一端通过导线与阻值为R=1Ω的电阻连接；导轨上放一质量为m=0.5kg的金属杆，金属杆与导轨的电阻均忽略不计．整个装置处于竖直向上的大小为B=0.5T的匀强磁场中．现用与导轨平行的拉力F作用在金属杆上，金属杆运动的v-t图象如图乙所示．（取重力加速度g=10m/s2）求：
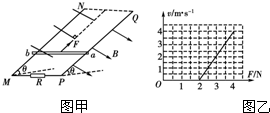如图甲所示，两根足够长的光滑直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上，两导轨间距为L．M、P两点间接有阻值为R的电阻．一根质量为m的均匀直金属杆ab放在两导轨上，并与导轨垂直．整套装置处于磁感应强度为B的匀强磁场中，磁场方向垂直斜面向下．导轨和金属杆的电阻可忽略．用与导轨平行且向上的恒定拉力F作用在金属杆上，金属杆ab沿导轨向上运动，最终将做匀速运动．当改变拉力F的大小时，相对应的匀速运动速度v也会改变，v和F的关系如图乙所示．
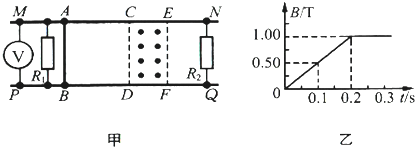（1）t=0.1s时电压表的读数；