题目内容
【题目】在光滑绝缘水平桌面上建立直角坐标系![]() ,y轴左侧有沿y轴正方向的匀强电场E,y轴右侧有垂直水平桌面向上的匀强磁场B.在
,y轴左侧有沿y轴正方向的匀强电场E,y轴右侧有垂直水平桌面向上的匀强磁场B.在![]() 处有一个带正电的小球A以速度
处有一个带正电的小球A以速度![]() 沿x轴正方向进入电场,运动一段时间后,从(0,8)处进入y轴右侧的磁场中,并且正好垂直于x轴进入第4象限,已知A球的质量为
沿x轴正方向进入电场,运动一段时间后,从(0,8)处进入y轴右侧的磁场中,并且正好垂直于x轴进入第4象限,已知A球的质量为![]() ,带电量为
,带电量为![]() ,求:
,求:

(1)电场强度E的大小;
(2)磁感应强度B的大小;
(3)如果在第4象限内静止放置一个不带电的小球C,使小球A运动到第4象限内与C球发生碰撞,碰后A、C粘在一起运动,则小球C放在何位置时,小球A在第4象限内运动的时间最长(小球可以看成是质点,不考虑碰撞过程中的电量损失).
【答案】(1)![]() (2)1.5T(3)
(2)1.5T(3)![]()
【解析】
(1)小球A在电场中沿x、y轴方向上的位移分别设为![]()

x方向:![]() ,
,
y方向:![]() ,
,
加速度:![]()
联立可得:![]()
(2)小球进入磁场时y方向的速度:![]() ,
,
合速度:![]() ,方向:
,方向:![]()
![]() ,方向与y轴正方向成
,方向与y轴正方向成![]()
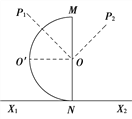
小球A在磁场中做匀速圆周运动,垂直于x轴进入第4象限,做出小球A运动的轨迹如图,设轨道半径为![]() ,由几何关系可得:
,由几何关系可得:![]()
根据:![]() ,解得:
,解得:![]()
(3)在第4象限内A与C球发生完全非弹性碰撞,碰撞后速度设为![]() ,在磁场中做圆周运动的轨道半径设为
,在磁场中做圆周运动的轨道半径设为![]() ,
,![]()
![]()
解得:![]()
即:小球运动的轨道半径不变
由周期公式![]() 可得:碰撞后小球的速度小,故碰后的周期大,所以要使小球A在第4象限内运动的时间最长,小球C应放在小球A进入第4象限时的位置:
可得:碰撞后小球的速度小,故碰后的周期大,所以要使小球A在第4象限内运动的时间最长,小球C应放在小球A进入第4象限时的位置:![]()
即坐标为![]()

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目