题目内容
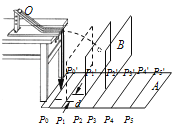
【题目】如图所示,某种变速自行车,有六个飞轮和三个链轮,链轮和飞轮的齿数如下表所示,后轮的直径为d=666mm . 当人骑该车,使脚踏板以恒定的角速度转动时,自行车行进的最大速度和最小速度之比为;当人骑该车行进的速度为v=4m/s时,脚踩踏板作匀速圆周运动的最小角速度是rad/s . 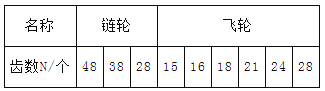

【答案】4;3
【解析】脚踏板以恒定的角速度转动时,当链轮的齿数最多,飞轮的齿数最少,自行车的行进速度最大;当链轮的齿数最少,飞轮的齿数最多,自行车的行驶速度最小.链轮和飞轮的轮半径与齿数成正比,因为是依靠同一个链条传动,所以链轮与飞轮的轮缘线速度是一样的,所以ω链r链=ω飞r飞 , 亦即ω链N链=ω飞N飞 . 当N链=48,N飞=12时,自行车速度最大,此时ω飞=4ω链 , 当N链=28 , N飞=28时,自行车速度最小,此时ω飞=ω链 , 而自行车的速度v ![]() ω , 所以自行车的最大速度和最小速度之比为4.
ω , 所以自行车的最大速度和最小速度之比为4.
当自行车行驶速度一定时,即后轮的角速度一定,飞轮的角速度一定,根据ω链N链=ω飞N飞 . 脚踏板和链轮有相同的角速度,知要使脚踩踏板作匀速圆周运动的角速度最小,则N链最多,N飞最少,即N链=48,N飞=12.
ω飞=ω后= ![]() ,所以ω脚=ω链=
,所以ω脚=ω链= ![]() =3.0rad/s .
=3.0rad/s .
故本题答案为:4,3.0.
【考点精析】解答此题的关键在于理解匀速圆周运动的相关知识,掌握匀速圆周运动线速度的大小恒定,角速度、周期和频率都是恒定不变的,向心加速度和向心力的大小也都是恒定不变的,是速度大小不变而速度方向时刻在变的变速曲线运动.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目