题目内容
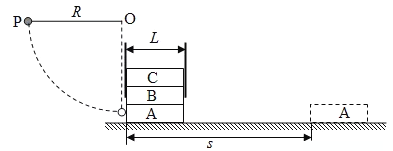
【题目】有一种打积木的游戏，装置如图所示，三块完全相同的积木叠放在靶位上，长为L，积木B与C夹在固定的两光滑薄板间，一钢球用长为R且不可伸长的轻绳挂于O点，钢球质量与每块积木的质量相等；游戏时，将钢球拉到与O等高的P点（保持绳绷直）由静止释放，钢球运动到最低点时与积木A发生弹性碰撞，积木A滑行一段距离s（
）后停下，又将钢球拉回P点由静止释放，与落下后静止的积木B发生弹性碰撞，积木B向前滑行与积木A碰撞后，以共同速度滑行一段距离后停止。已知重力加速度为g，各接触面间的动摩擦因数相同，碰撞时间极短。求
（1）钢球与积木A碰撞前、后瞬间的速度大小；
（2）动摩擦因数；
（3）积木B滑行的距离。
【答案】（1）
0（2）
（3）
【解析】
（1）设钢球和滑块的质量均为m，由机械能守恒定律可得：
解得
钢球与滑块A碰撞过程满足：
解得
v1=0，
（2）对滑块A由动能定理：
解得
（3）又将钢球拉回P点由静止释放，与落下后静止的积木B发生弹性碰撞，此时B的速度仍为
滑行s-L后与A碰撞，此时B的速度：
当AB碰撞时，由动量守恒：
解得
由动能定理：
解得
，
则积木B滑行的距离
练习册系列答案
阅读快车系列答案
相关题目
