题目内容
2. 如图所示,一个绝缘且内壁光滑的环形细圆管,固定于竖直平面内,环的半径为R(比细管的内径大得多),在圆管内的最低点有一个直径略小于细管内径的带正电小球处于静止状态,小球的质量为m,带电荷量为q,重力加速度为g.空间存在一磁感应强度大小未知(不为零),方向垂直于环形细圆管所在平面且向里的匀强磁场.某时刻,给小球一方向水平向右,大小为v0=$\sqrt{5gR}$的初速度,则以下判断正确的是( )
如图所示,一个绝缘且内壁光滑的环形细圆管,固定于竖直平面内,环的半径为R(比细管的内径大得多),在圆管内的最低点有一个直径略小于细管内径的带正电小球处于静止状态,小球的质量为m,带电荷量为q,重力加速度为g.空间存在一磁感应强度大小未知(不为零),方向垂直于环形细圆管所在平面且向里的匀强磁场.某时刻,给小球一方向水平向右,大小为v0=$\sqrt{5gR}$的初速度,则以下判断正确的是( )| A. | 无论磁感应强度大小如何,获得初速度后的瞬间,小球在最低点一定受到管壁的弹力作用 | |
| B. | 无论磁感应强度大小如何,小球一定能到达环形细管的最高点,小球在最高点不一定受到管壁的弹力作用 | |
| C. | 无论磁感应强度大小如何,小球一定能到达环形细管的最高点,且小球到达最高点时的速度大小都相同 | |
| D. | 小球在从环形细圆管的最低点运动到所能到达的最高点的过程中,机械能不守恒 |
分析 由左手定则可判定小球受到的洛伦兹力始终指向圆心,对受力分析,结合圆周运动方程可分析小球是不是受到弹力;
由于洛伦兹力不做功,由动能定理可判定小球是否能到最高点;
由曲线运动的速度方向,以及速度的分解可以判定小球运动过程中,水平速度的变化
解答 解:A、由左手定则可判定小球受到的洛伦兹力F始终指向圆心,另外假设小球受到管道的支持力N,小球获得v0=$\sqrt{5gR}$的初速度后,由圆周运动可得:F+N-mg=$\frac{{mv}_{0}^{2}}{R}$
解得:N=mg+$\frac{{mv}_{0}^{2}}{R}$-F=mg+$\frac{{mv}_{0}^{2}}{R}$-qv0B
可见,只要B足够大,满足mg+$\frac{{mv}_{0}^{2}}{R}$=qv0B,支持力N就为零,故A错误.
BC、由于洛伦兹力不做功,只有重力对小球做功,故小球能不能到最高点与磁感应强度大小无关,从最低点到最高抵过程中,由动能定理可得:
-mg2R=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02
解得:v=$\sqrt{gR}$,
可知小球能到最高点,由于当v=$\sqrt{gR}$,小球受到的向心力等于mg,故此时小球除受到重力,向下的洛伦兹力之外,一定还有轨道向上的支持力大小等于洛伦兹力,故B错误,C正确.
D、对小球的速度分解在水平和竖直方向上,小球在从环形细圆管的最低点运动到所能到达的最高点的过程中,水平方向分速度先减小,至圆心等高处,水平分速度为零,再往上运动,水平分速度又增加,故D错误.
故选:C
点评 该题要注意洛伦兹力不做功,只改变速度方向,掌握基本的圆周运动公式,要知道一个临界问题,即最高点时,重力充当向心力,v=$\sqrt{gR}$


| A. | 小球受到重力、弹力和向心力作用 | |
| B. | 小球受到重力和弹力作用 | |
| C. | 小球只受到一个水平指向圆心的向心力作用 | |
| D. | 小球受到重力和弹力的合力是恒力 |
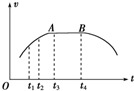 一个带正电的点电荷仅在电场力作用下在某空间运动,其速度-时间图象如图所示,其中t1、t2、t3、t4是电荷在电场中运动的1、2、3、4点对应的四个时刻,图中AB与时间轴平行,则下列说法正确的是( )
一个带正电的点电荷仅在电场力作用下在某空间运动,其速度-时间图象如图所示,其中t1、t2、t3、t4是电荷在电场中运动的1、2、3、4点对应的四个时刻,图中AB与时间轴平行,则下列说法正确的是( )| A. | 电场中1、2两点处电场强度大小E1<E2 | |
| B. | 电场中3、4两点处电场强度大小为零 | |
| C. | 电场中2、4两点电势φ2>φ4 | |
| D. | 电荷从1运动到3的过程中,电场力做负功,电势能增加 |
 如图所示的电路中,各个电阻都是2Ω,电流表内阻不计,在B、C两点间加6V电压时,则电流表的示数为( )
如图所示的电路中,各个电阻都是2Ω,电流表内阻不计,在B、C两点间加6V电压时,则电流表的示数为( )| A. | 0.5A | B. | 1A | C. | 1.5A | D. | 2A |
| A. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法是微元法 | |
| B. | 根据速度定义式v=$\frac{△x}{△t}$,当△t→0时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义运用了极限思维法 | |
| C. | 在探究加速度、力和质量三者之间的关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系,这里运用了假设法 | |
| D. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,再把各小段位移相加,这里运用了理想模型法 |
 如图所示,已充电的平行板电容器,带正电的极板接地,两极板间于P点处固定一负的点电荷,若将上极板下移至虚线位置,则下列说法中正确的是( )
如图所示,已充电的平行板电容器,带正电的极板接地,两极板间于P点处固定一负的点电荷,若将上极板下移至虚线位置,则下列说法中正确的是( )| A. | 两极间的电压和板间场强都变小 | |
| B. | 两极间的电压变小,但场强不变 | |
| C. | P点的电势升高,点电荷的电势能增大 | |
| D. | P点的电势不变,点电荷的电势能也不变 |
 如图所示,质量为M的小车的上表面由均匀粗糙的水平段ac和光滑的四分之一圆弧段cd组成,b是ac段的中点,小车静止在光滑的水平面上,一质量为m的小物块(可视为质点)从小车左端点a处以水平初速度v0冲上小车水平段.如果小车固定,小物块恰好能返回a处,如果小车不固定,下列是否正确的是( )
如图所示,质量为M的小车的上表面由均匀粗糙的水平段ac和光滑的四分之一圆弧段cd组成,b是ac段的中点,小车静止在光滑的水平面上,一质量为m的小物块(可视为质点)从小车左端点a处以水平初速度v0冲上小车水平段.如果小车固定,小物块恰好能返回a处,如果小车不固定,下列是否正确的是( )| A. | 小物块还是恰好能返回a处 | |
| B. | 小物块一定能通过c处再返回 | |
| C. | 如果M=m,小物块一定相对小车停在b处 | |
| D. | 如果M=m,小物块一定相对小车停在c处 |
 如图所示,有一根金属棒ab与竖直放置的金属线框接触良好,且无摩擦,整个线框处在方向垂直于纸面的匀强磁场中.要使ab棒保持静止,框架应当在竖直方向上平动.
如图所示,有一根金属棒ab与竖直放置的金属线框接触良好,且无摩擦,整个线框处在方向垂直于纸面的匀强磁场中.要使ab棒保持静止,框架应当在竖直方向上平动. 如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,然后小球从轨道口B处飞出,最后落在水平面上,已知小球落地点C距B处的距离为3R.求:
如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,然后小球从轨道口B处飞出,最后落在水平面上,已知小球落地点C距B处的距离为3R.求: