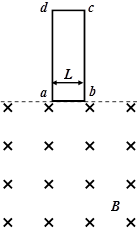题目内容
如图所示,一质量m=0.10kg、电阻R=0.10Ω的矩形金属框abcd由静止开始释放,竖直向下进入匀强磁场。已知磁场方向垂直纸面向内,磁感应强度B=0.50T,金属框宽L=0.20m,开始释放时ab边与磁场的上边界重合。经过时间t1,金属框下降了h1=0.50m,金属框中产生了Q1=0.45J的热量,取g=10m/s2。
(1)求经过时间t1时金属框速度v1的大小以及感应电流的大小和方向;
(2)经过时间t1后,在金属框上施加一个竖直方向的拉力,使它作匀变速直线运动,再经过时间t2=0.1s,又向下运动了h2=0.12m,求金属框加速度的大小以及此时拉力的大小和方向(此过程中cd边始终在磁场外)。
(3)t2时间后该力变为恒定拉力,又经过时间t3金属框速度减小到零后不再运动。求该拉力的大小以及t3时间内金属框中产生的焦耳热(此过程中cd边始终在磁场外)。
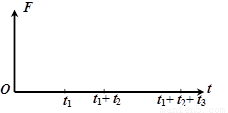 (4)在所给坐标中定性画出金属框所受安培力F随时间t变化的关系图线。
(4)在所给坐标中定性画出金属框所受安培力F随时间t变化的关系图线。
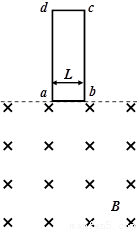
【答案】
(1)1A(2)1.4m/s -0.46N,方向向上(3)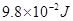 (4)见解析
(4)见解析
【解析】(1)(4分)由功能关系

得 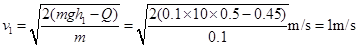
 ,
逆时针方向
,
逆时针方向
(2)(6分)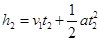

t2=0.1s时,金属框的速度 v2=v1+at2=(1+4.0×0.1)m/s=1.4m/s
此时金属框的电流 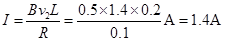
由牛顿第二定律 F2+mg – BIL=ma
F2=ma+BIL – mg= -0.46N , (1分) 方向向上
(3)(2分)金属框做加速度运动最后静止,所加恒定的外力等于重力F=mg=1N
金属框只在安培力作用下做减速运动,动能全部转化为焦耳热,

 (4)(2分)
(4)(2分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

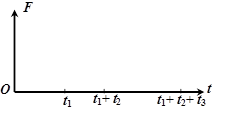 (4)在所给坐标中定性画出金属框所受安培力F随时间t变化的关系图线。
(4)在所给坐标中定性画出金属框所受安培力F随时间t变化的关系图线。