题目内容
8. 如图所示,AB、AC两光滑细杆组成的直角支架固定在竖直平面内,AB与水平面的夹角为30°,两细杆上分别套有带孔的a、b两小球(可视为质点),在细线作用下处于静止状态,细线恰好水平.某时刻剪断细线,在两球下滑到底端的过程中,下列结论中正确的是( )
如图所示,AB、AC两光滑细杆组成的直角支架固定在竖直平面内,AB与水平面的夹角为30°,两细杆上分别套有带孔的a、b两小球(可视为质点),在细线作用下处于静止状态,细线恰好水平.某时刻剪断细线,在两球下滑到底端的过程中,下列结论中正确的是( )| A. | a、b两球到底端时速度相同 | |
| B. | a、b两球重力做功之比为3:1 | |
| C. | 小球a受到的弹力等于小球b受到的弹力 | |
| D. | 小球a下滑的时间与小球b下滑的时间之比为$\sqrt{3}$:1 |
分析 a、b两球到底端时速度的方向沿各自斜面的方向;根据位移公式计算下滑的时间.
重力做功W=mgh,根据平衡条件比较质量的大小;则可得出重力做功的大小.
解答 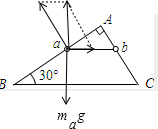 解:A、由机械能守恒定律可知:mgh=$\frac{1}{2}$mv2;解得:v=$\sqrt{2gh}$;故到达底部时速度的大小相同;但是方向不同.故A错误;
解:A、由机械能守恒定律可知:mgh=$\frac{1}{2}$mv2;解得:v=$\sqrt{2gh}$;故到达底部时速度的大小相同;但是方向不同.故A错误;
B、根据平衡条件:mag=$\frac{T}{tan30°}$
同理可得:mbg=$\frac{T}{tan60°}$
故ma:mb=3:1
小球到底端的过程中重力做的功:W=mgh,则a、b两球重力做功之比为3:1,故B正确;
C、小球a受到的弹力为:N=magcos30°=3mg$•\frac{\sqrt{3}}{2}$
小球b受到的弹力为:N′=mbgcos60°=mg•$\frac{1}{2}$
故a受到的弹力大于球b受到的弹力;故C错误;
D、设从斜面下滑的高度为h,则有:$\frac{h}{sin30°}$=$\frac{1}{2}$at2
aa=gsin30°
得:t=$\frac{\sqrt{2h}}{\sqrt{g}sin30°}$
同理:$\frac{h}{sin60°}$=$\frac{1}{2}$gsin60°t′2
t′=$\frac{\sqrt{2h}}{\sqrt{g}sin60°}$
可见a球下滑的时间较长,故D正确;
故选:BD.
点评 本题考查动能定理及共点力的平衡条件,关键是找出二球静止时绳子对两球的拉力是相同的,进而可以比较二者重力的大小关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.甲、乙两车在平直公路上沿同一方向行驶,其v-t图象如图所示,在 t=0时刻,乙车在甲车前方x0处,在t=t1时间内甲车的位移为x.下列判断正确的是( )
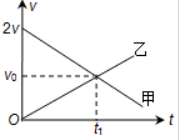

| A. | 若甲、乙在t1时刻相遇,则x0=$\frac{2}{3}$x | |
| B. | 若甲、乙在$\frac{{t}_{1}}{2}$时刻相遇,则下次相遇时刻为$\frac{3}{2}$t1 | |
| C. | 若x0=$\frac{3}{4}$x,则甲、乙一定相遇两次 | |
| D. | 若x0=$\frac{1}{2}$x,则甲、乙一定不能相遇 |
16. 如图,倾角为α的斜面上放置着光滑导轨,金属棒KN置于导轨上,在以ab和cd为边界的区域内存在磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向上.在cd左侧的无磁场区域cdPM内有一半径很小的金属圆环L,圆环与导轨在同一平面内.当金属棒KN在重力作用下从磁场右边界ab处由静止开始向下运动后,则下列说法正确的是( )
如图,倾角为α的斜面上放置着光滑导轨,金属棒KN置于导轨上,在以ab和cd为边界的区域内存在磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向上.在cd左侧的无磁场区域cdPM内有一半径很小的金属圆环L,圆环与导轨在同一平面内.当金属棒KN在重力作用下从磁场右边界ab处由静止开始向下运动后,则下列说法正确的是( )
 如图,倾角为α的斜面上放置着光滑导轨,金属棒KN置于导轨上,在以ab和cd为边界的区域内存在磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向上.在cd左侧的无磁场区域cdPM内有一半径很小的金属圆环L,圆环与导轨在同一平面内.当金属棒KN在重力作用下从磁场右边界ab处由静止开始向下运动后,则下列说法正确的是( )
如图,倾角为α的斜面上放置着光滑导轨,金属棒KN置于导轨上,在以ab和cd为边界的区域内存在磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向上.在cd左侧的无磁场区域cdPM内有一半径很小的金属圆环L,圆环与导轨在同一平面内.当金属棒KN在重力作用下从磁场右边界ab处由静止开始向下运动后,则下列说法正确的是( )| A. | 圆环L有收缩趋势 | B. | 圆环L有扩张趋势 | ||
| C. | 圆环内产生的感应电流变小 | D. | 圆环内产生的感应电流不变 |
3.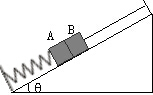 如图所示,在倾角为θ=30°的光滑斜面上,物块A、B质量分别为m和2m.物块A静止在轻弹簧上面,物块B用细线与斜面顶端相连,A、B紧挨在一起但A、B之间无弹力,已知重力加速度为g,某时刻把细线剪断,当细线剪断瞬间,下列说法正确的是( )
如图所示,在倾角为θ=30°的光滑斜面上,物块A、B质量分别为m和2m.物块A静止在轻弹簧上面,物块B用细线与斜面顶端相连,A、B紧挨在一起但A、B之间无弹力,已知重力加速度为g,某时刻把细线剪断,当细线剪断瞬间,下列说法正确的是( )
 如图所示,在倾角为θ=30°的光滑斜面上,物块A、B质量分别为m和2m.物块A静止在轻弹簧上面,物块B用细线与斜面顶端相连,A、B紧挨在一起但A、B之间无弹力,已知重力加速度为g,某时刻把细线剪断,当细线剪断瞬间,下列说法正确的是( )
如图所示,在倾角为θ=30°的光滑斜面上,物块A、B质量分别为m和2m.物块A静止在轻弹簧上面,物块B用细线与斜面顶端相连,A、B紧挨在一起但A、B之间无弹力,已知重力加速度为g,某时刻把细线剪断,当细线剪断瞬间,下列说法正确的是( )| A. | 物块A的加速度为0 | B. | 物块A的加速度为$\frac{g}{3}$ | ||
| C. | 物块B的加速度为0 | D. | 物块B的加速度为$\frac{g}{2}$ |
20.一个电荷量为1.0×10-7C的负电荷从电场中A点移动到B点时电场力做功2.0×10-7J,从C点移动到D点时克服电场力做功7.0×10-7J.若已知B点比C点的电势高3V,则下列关于各点间的电势差关系正确的是( )
| A. | UAB=2V | B. | UCD=-7V | C. | UBD=-3V | D. | UAC=1V |
15.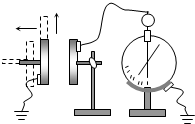 如图所示为研究影响平行板电容器电容大小因素的实验装置.实验中极板所带电荷量可视为不变.则下列关于实验的分析正确的是( )
如图所示为研究影响平行板电容器电容大小因素的实验装置.实验中极板所带电荷量可视为不变.则下列关于实验的分析正确的是( )
 如图所示为研究影响平行板电容器电容大小因素的实验装置.实验中极板所带电荷量可视为不变.则下列关于实验的分析正确的是( )
如图所示为研究影响平行板电容器电容大小因素的实验装置.实验中极板所带电荷量可视为不变.则下列关于实验的分析正确的是( )| A. | 只将左极板从图示位罝稍向左平移,静电计指针张角变大 | |
| B. | 只在两极板间插人云母板,静电计指针张角变大 | |
| C. | 只将左极板从图示位置稍向上平移,静电计指针张角不变 | |
| D. | 只将左极板从图示位置稍向上平移,静电计指针张角变大 |
15. 如图所示,重为100N的物体,以初速度v0沿水平面向右滑行,同时受水平向左的外力F=20N作用.已知物体与水平面的动摩擦因数为0.2,则此时物体所受的摩擦力为( )
如图所示,重为100N的物体,以初速度v0沿水平面向右滑行,同时受水平向左的外力F=20N作用.已知物体与水平面的动摩擦因数为0.2,则此时物体所受的摩擦力为( )
 如图所示,重为100N的物体,以初速度v0沿水平面向右滑行,同时受水平向左的外力F=20N作用.已知物体与水平面的动摩擦因数为0.2,则此时物体所受的摩擦力为( )
如图所示,重为100N的物体,以初速度v0沿水平面向右滑行,同时受水平向左的外力F=20N作用.已知物体与水平面的动摩擦因数为0.2,则此时物体所受的摩擦力为( )| A. | 0 | B. | 40N,水平向左 | C. | 20N,水平向右 | D. | 20N,水平向左 |
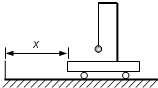 如图所示,小车上有一个固定支架,支架上用长为L的绝缘细线悬挂质量为m、电量为+q的小球,处于水平方向的匀强电场中(图中未画出),小车在竖直固定挡板右侧某处,向着挡板从静止开始做加速度a=g的匀加速直线运动,此过程细线刚好保持竖直,当小车碰到挡板就立即停止运动,且此时电场方向为竖直向下,电场强度大小保持不变.求小车停止后.
如图所示,小车上有一个固定支架,支架上用长为L的绝缘细线悬挂质量为m、电量为+q的小球,处于水平方向的匀强电场中(图中未画出),小车在竖直固定挡板右侧某处,向着挡板从静止开始做加速度a=g的匀加速直线运动,此过程细线刚好保持竖直,当小车碰到挡板就立即停止运动,且此时电场方向为竖直向下,电场强度大小保持不变.求小车停止后.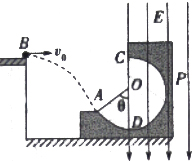 如图所示,P是固定在水平面上的圆弧轨道,O是圆弧的圆心,C为圆弧轨道最高点,D为圆弧轨道最低点,从高台边B点以速度v0水平飞出质量为m、带电量为+q的小球,恰能从圆弧轨道的左端A点沿圆弧切线方向进入,θ是OA与竖直方向的夹角,圆弧轨道的竖直直径COD右边存在竖直向下的匀强电场,电场强度为E,已知:m=1kg,v0=3m/s,q=1.6×10-4C,E=104V/m,θ=53°,g=10m/s2,sin37°=0.6,cos37°=0.8.若小球恰能到达最高点C,不计空气阻力和所有摩擦.求:
如图所示,P是固定在水平面上的圆弧轨道,O是圆弧的圆心,C为圆弧轨道最高点,D为圆弧轨道最低点,从高台边B点以速度v0水平飞出质量为m、带电量为+q的小球,恰能从圆弧轨道的左端A点沿圆弧切线方向进入,θ是OA与竖直方向的夹角,圆弧轨道的竖直直径COD右边存在竖直向下的匀强电场,电场强度为E,已知:m=1kg,v0=3m/s,q=1.6×10-4C,E=104V/m,θ=53°,g=10m/s2,sin37°=0.6,cos37°=0.8.若小球恰能到达最高点C,不计空气阻力和所有摩擦.求: