题目内容
（1）某同学用半圆形玻璃砖测定玻璃的折射率（如图所示）．实验的主要过程如下：
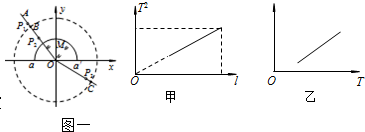
a．把白纸用图钉钉在木板上，在白纸上作出直角坐标系xOy，在白纸上画一条线段 AO表示入射光线．
b．把半圆形玻璃砖M放在白纸上，使其底边aa′与Ox轴重合．
c．用一束平行于纸面的激光从y＞0区域沿y轴负方向射向玻璃砖，并沿x轴方向调整玻璃砖的位置，使这束激光从玻璃砖底面射出后，仍沿y轴负方向传播．
d．在AO线段上竖直地插上两枚大头针P1、P2．
e．在坐标系的y＜0的区域内竖直地插上大头针P3，并使得从P3一侧向玻璃砖方向看去，P3能同时挡住观察P1和P2的视线．
f．移开玻璃砖，作OP3连线，用圆规以O点为圆心画一个圆（如图中虚线所示），此圆与AO线交点为B，与OP3连线的交点为C．确定出B点到x轴、y轴的距离分别为x1、y1、，C点到x轴、y轴的距离分别为x2、y2．
①根据上述所确定出的B、C两点到两坐标轴的距离，可知此玻璃折射率测量值的表达式为n= ．
②若实验中该同学在y＜0的区域内，从任何角度都无法透过玻璃砖看到P1、P2，其原因可能是： ．
（2）在“用单摆测重力加速度”的实验中，某同学的主要操作步骤如下：
a．取一根符合实验要求的摆线，下端系一金属小球，上端固定在O点；
b．在小球静止悬挂时测量出O点到小球球心的距离l；
c．拉动小球使细线偏离竖直方向一个不大的角度（约为5°），然后由静止释放小球；
d．用秒表记录小球完成n次全振动所用的时间t．
①用所测物理量的符号表示重力加速度的测量值，其表达式为g= ；
②若测得的重力加速度数值大于当地的重力加速度的实际值，造成这一情况的原因可能是 ．（选填下列选项前的序号）
A．测量摆长时，把摆线的长度当成了摆长
B．摆线上端未牢固地固定于O点，振动中出现松动，使摆线越摆越长
C．测量周期时，误将摆球（n-1）次全振动的时间t记为了n次全振动的时间，并由计算式T=t/n求得周期
D．摆球的质量过大
③在与其他同学交流实验方案并纠正了错误后，为了减小实验误差，他决定用图象法处理数据，并通过改变摆长，测得了多组摆长l和对应的周期T，并用这些数据作出T2-l图象如图甲所示．若图线的斜率为k，则重力加速度的测量值g= ．
④这位同学查阅资料得知，单摆在最大摆角θ较大时周期公式可近似表述为T=2π
（1+
sin2
）．为了用图象法验证单摆周期T和最大摆角θ的关系，他测出摆长为l的同一单摆在不同最大摆角θ时的周期T，并根据实验数据描绘出如图乙所示的图线．根据周期公式可知，图乙中的纵轴表示的是 ，图线延长后与横轴交点的横坐标为 ．
a．把白纸用图钉钉在木板上，在白纸上作出直角坐标系xOy，在白纸上画一条线段 AO表示入射光线．
b．把半圆形玻璃砖M放在白纸上，使其底边aa′与Ox轴重合．
c．用一束平行于纸面的激光从y＞0区域沿y轴负方向射向玻璃砖，并沿x轴方向调整玻璃砖的位置，使这束激光从玻璃砖底面射出后，仍沿y轴负方向传播．
d．在AO线段上竖直地插上两枚大头针P1、P2．
e．在坐标系的y＜0的区域内竖直地插上大头针P3，并使得从P3一侧向玻璃砖方向看去，P3能同时挡住观察P1和P2的视线．
f．移开玻璃砖，作OP3连线，用圆规以O点为圆心画一个圆（如图中虚线所示），此圆与AO线交点为B，与OP3连线的交点为C．确定出B点到x轴、y轴的距离分别为x1、y1、，C点到x轴、y轴的距离分别为x2、y2．
①根据上述所确定出的B、C两点到两坐标轴的距离，可知此玻璃折射率测量值的表达式为n=
②若实验中该同学在y＜0的区域内，从任何角度都无法透过玻璃砖看到P1、P2，其原因可能是：
（2）在“用单摆测重力加速度”的实验中，某同学的主要操作步骤如下：
a．取一根符合实验要求的摆线，下端系一金属小球，上端固定在O点；
b．在小球静止悬挂时测量出O点到小球球心的距离l；
c．拉动小球使细线偏离竖直方向一个不大的角度（约为5°），然后由静止释放小球；
d．用秒表记录小球完成n次全振动所用的时间t．
①用所测物理量的符号表示重力加速度的测量值，其表达式为g=
②若测得的重力加速度数值大于当地的重力加速度的实际值，造成这一情况的原因可能是
A．测量摆长时，把摆线的长度当成了摆长
B．摆线上端未牢固地固定于O点，振动中出现松动，使摆线越摆越长
C．测量周期时，误将摆球（n-1）次全振动的时间t记为了n次全振动的时间，并由计算式T=t/n求得周期
D．摆球的质量过大
③在与其他同学交流实验方案并纠正了错误后，为了减小实验误差，他决定用图象法处理数据，并通过改变摆长，测得了多组摆长l和对应的周期T，并用这些数据作出T2-l图象如图甲所示．若图线的斜率为k，则重力加速度的测量值g=
④这位同学查阅资料得知，单摆在最大摆角θ较大时周期公式可近似表述为T=2π
|
| 1 |
| 4 |
| θ |
| 2 |
分析：（1）①根据折射定律n=
结合几何关系求解；②若从任何角度都无法透过玻璃砖看到P1、P2，其原因可能是入射光发生了全反射；
（2）根据单摆的周期公式，得到重力加速度的表达式，再分析造成重力加速度测量值偏大的原因．由单摆周期公式的变形公式求出T2-L关系表达式，即可求g，图象是一次函数，表示成线性关系．
| sini |
| sinr |
（2）根据单摆的周期公式，得到重力加速度的表达式，再分析造成重力加速度测量值偏大的原因．由单摆周期公式的变形公式求出T2-L关系表达式，即可求g，图象是一次函数，表示成线性关系．
解答：解：（1）①设圆的半径为R，根据几何知识得，sinr=
，sini=
根据折射定律n=
得：
n=
②若从任何角度都无法透过玻璃砖看到P1、P2，其原因可能是沿P1、P2方向入射光在玻璃砖底边的界面上发生了全反射；
（2）根据已知条件可知，T=
，
根据单摆的周期公式得：
T=2π
解得：g=
A、测量摆长时，把摆线长当成摆长时，摆长l偏小，测得的重力加速度数值应小于实际值．故A错误．
B、摆线上端没有系牢，摆动过程因松动而使摆线变长，则所测单摆的实际周期T偏大，所以所测重力加速度偏小，故B错误；
C、将摆球（n-1）次全振动的时间t记为了n次全振动的时间，根据g=
可知，g偏大，故C正确；
D、重力加速度与摆球质量无关，故D错误；
故选C
③根据单摆的周期公式得：
T=2π
所以T2=4π2
=
L，所以T2-L图象中的斜率k=
，即g=
④实验中得到的线性图线，根据T=2π
（1+
sin2
）得：sin2
=
T-4，所以sin2
与T成一次函数关系，
所以图乙中的纵轴表示的是sin2
，图线延长后与横轴交点的横坐标为2π
故答案为：（1）
；沿P1、P2方向入射光在玻璃砖底边的界面上发生了全反射；（2）
；C；
；sin2
；2π
| x1 |
| R |
| x2 |
| R |
根据折射定律n=
| sini |
| sinr |
n=
| x2 |
| x1 |
②若从任何角度都无法透过玻璃砖看到P1、P2，其原因可能是沿P1、P2方向入射光在玻璃砖底边的界面上发生了全反射；
（2）根据已知条件可知，T=
| t |
| n |
根据单摆的周期公式得：
T=2π
|
解得：g=
| 4π2n2l |
| t2 |
A、测量摆长时，把摆线长当成摆长时，摆长l偏小，测得的重力加速度数值应小于实际值．故A错误．
B、摆线上端没有系牢，摆动过程因松动而使摆线变长，则所测单摆的实际周期T偏大，所以所测重力加速度偏小，故B错误；
C、将摆球（n-1）次全振动的时间t记为了n次全振动的时间，根据g=
| 4π2n2l |
| t2 |
D、重力加速度与摆球质量无关，故D错误；
故选C
③根据单摆的周期公式得：
T=2π
|
所以T2=4π2
| L |
| g |
| 4π2 |
| g |
| 4π2 |
| g |
| 4π2 |
| k |
④实验中得到的线性图线，根据T=2π
|
| 1 |
| 4 |
| θ |
| 2 |
| θ |
| 2 |
| 2 | ||||
π
|
| θ |
| 2 |
所以图乙中的纵轴表示的是sin2
| θ |
| 2 |
|
故答案为：（1）
| x2 |
| x1 |
| 4π2n2l |
| t2 |
| 4π2 |
| k |
| θ |
| 2 |
|
点评：（1）本题采用单位圆法测量玻璃砖的折射率，是数学知识在物理实验中的运用，简单方便．（2）解决本题的关键掌握单摆的周期公式T=2π
，会通过g=
，分析因摆长、周期的误差而引起重力加速度的误差．
|
| 4π2 l |
| T2 |
练习册系列答案
阅读快车系列答案
相关题目
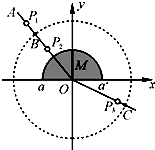某同学用半圆形玻璃砖测定玻璃的折射率（如图所示）．实验的主要步骤如下：
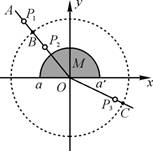
（1+
sin2
）．为了用图象法验证单摆周期T和最大摆角θ的关系，他测出摆长为l的同一单摆在不同最大摆角θ时的周期T，并根据实验数据描绘出如图乙所示的图线．根据周期公式可知，图乙中的纵轴表示的是______，图线延长后与横轴交点的横坐标为______