题目内容
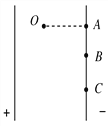
【题目】如图所示，质量为m的小球(可视为质点)用长为L的细线悬挂于O点，自由静止在A位置．现用水平力F缓慢地将小球从A拉到B位置而静止，细线与竖直方向夹角为θ＝60°，此时细线的拉力为T1，然后撤去水平力F，小球从B返回到A点时细线的拉力为T2，则( )
A. T1＝T2＝2mg
B. 从A到B，拉力F做功为mgL
C. 从B到A的过程中，小球受到的合外力大小不变
D. 从B到A的过程中，小球重力的瞬时功率先增大后减小
【答案】AD
【解析】小球在B位置时受到向下的重力mg、水平向左的拉力F、沿BO方向的拉力T1，根据平衡条件应有
；小球返回到A时，根据牛顿第二定律应有
从B到A由动能定理可得mgL（1-cos60°）=
mvA20；联立可得T2=2mg，即T1=T2=2mg
，所以A正确；根据动能定理应有WF-mgL（1-cos60°）=0，解得WF=
mgL，所以B错误；从B到A小球做圆周运动，在B点时所受的合力为FB=mgsinθ，在A点时所受的合力为
，再由动能定理mgL（1-cosθ）=
mvA2，解得FA=2mg（1-cosθ），显然FA≠FB
，所以C错误；根据P=Fvcosα，小球在B点时的速度为0，所以重力的瞬时功率也为0，尽管小球在A点时的速度最大，但此时在竖直方向的速度为0，所以重力的瞬时功率也为0，所以小球从B到A的过程中重力的瞬时功率应先增大后减小，D正确；故选AD．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
