题目内容
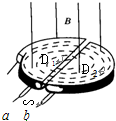回旋加速器是加速带电粒子的装置，其主体部分是两个D形金属盒．两金属盒处在垂直于盒底的匀强磁场中，a、b分别与高频交流电源两极相连接，下列说法正确的是（ ）分析：回旋加速器中带电粒子在电场被加速，每通过电场，动能被增加一次；而在磁场里做匀速圆周运动，通过磁场时只改变粒子的运动方向，动能却不变．因此带电粒子在一次加速过程中，电场电压越大，动能增加越大．但从D形盒中射出的动能，除与每次增加的动能外，还与加速次数有关．所以加速电压越大，回旋次数越少，推导出最大动能的表达式，分析最大动能与磁感应强度和D形金属盒半径的关系．
解答：解：A、离子在磁场中受到洛伦兹力，但不做功，故A错误；
B、带电粒子源源不断的处于加速状态，虽速度增大，但在磁场中周期不变，所以粒子的运动周期是固定的，故B错误；
C、离子由加速器的中心附近进入电场中加速后，进入磁场中偏转．故C正确；
带电粒子从D形盒中射出时的动能 Ekm=
mvm2 （1）
带电粒子在磁场中做匀速圆周运动，则圆周半径 R=
（2）
由（1）（2）可得Ekm=
显然，当带电粒子q、m一定的，则Ekm∝R2 B2
即Ekm随磁场的磁感应强度B、D形金属盒的半径R的增大而增大，与加速电场的电压和狭缝距离无关，故D错误；
故选C．
B、带电粒子源源不断的处于加速状态，虽速度增大，但在磁场中周期不变，所以粒子的运动周期是固定的，故B错误；
C、离子由加速器的中心附近进入电场中加速后，进入磁场中偏转．故C正确；
带电粒子从D形盒中射出时的动能 Ekm=
| 1 |
| 2 |
带电粒子在磁场中做匀速圆周运动，则圆周半径 R=
| mvm |
| qB |
由（1）（2）可得Ekm=
| q2B2R2 |
| 2m |
即Ekm随磁场的磁感应强度B、D形金属盒的半径R的增大而增大，与加速电场的电压和狭缝距离无关，故D错误；
故选C．
点评：本题回旋加速器考查电磁场的综合应用：在电场中始终被加速，在磁场中总是匀速圆周运动．所以容易让学生产生误解：增加射出的动能由加速电压与缝间决定．原因是带电粒子在电场中动能被增加，而在磁场中动能不变．
练习册系列答案
相关题目
（2008?武昌区模拟）回旋加速器是加速带电粒子的装置，其核心部分是分别与高频交流电极相连接的两个D形金属盒，两盒间的狭缝中形成的周期性变化的电场，使粒子在通过狭缝时都能得到加速，两D形金属盒处于垂直于盒底的匀强磁场中，如图所示，要增大带电粒子射出时的动能，则下列说法中正确的是（ ）
回旋加速器是加速带电粒子的装置，其核心部分是分别与高频交流电极相连接的两个D形金属盒，两盒间的狭缝中形成周期性变化的电场，使粒子在通过狭缝时都能得到加速，两D形金属盒处于垂直于盒底的匀强磁场中，如图所示，则下列说法正确的是（ ）
（2012?丹东模拟）回旋加速器是加速带电粒子的装置，其核心部分是分别与高频交流电源两极相连接的两个D形金属盒，两盒间的狭缝中形成周期性变化的电场，使粒子在通过狭缝时都能得到加速，两D形金属盒处于垂直于盒底的匀强磁场中，如图所示．设D形盒半径为R．若用回旋加速器加速质子时，匀强磁场的磁感应强度为B，高频交流电频率为f．则下列说法正确的是（ ）
回旋加速器是加速带电粒子的装置，其核心部分是分别与高频交流电两极相连接的两个D形金属盒，两盒间的狭缝中形成的周期性变化的匀强电场，使粒子在通过狭缝时都能得到加速．两D形金属盒处于垂直于盒底面的匀强磁场中，如图所示，设匀强磁场的磁感应强度为B，D形金属盒的半径为R，狭缝间的距离为d，匀强电场间的加速电压为U，要增大带电粒子（电荷量为q质量为m，不计重力）射出时的动能，则下列方法中正确的是（ ）| A、增大匀强电场间的加速电压 | B、减小狭缝间的距离 | C、增大磁场的磁感应强度 | D、增大D形金属盒的半径 |
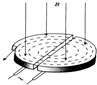回旋加速器是加速带电粒子的装置，其核心部分是分别与高频交流电源两极相连接的两个D形金属盒，两盒间的狭缝中形成周期性变化的电场，使粒子在通过狭缝时都能得到加速，两D形金属盒处于垂直于盒底的匀强磁场中，如图所示．设D形盒半径为R．若用回旋加速器加速质子（氢核）时，匀强磁场的磁感应强度为B，高频交流电频率为f．质子质量为m，电荷量为e．则下列说法正确的是（ ）| A、质子被加速后的最大速度不可能超过2πRf | ||
B、质子被加速后的最大动能Ek不可能超过
| ||
| C、质子被加速后的最大动能与狭缝间的加速电压、加速次数无关 | ||
| D、改变B和f，该回旋加速器也能用于加速α粒子（即氦核） |