题目内容
18.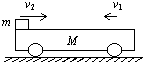 质量为M=4m的小车以v1=0.50m/s沿光滑水平面向左运动.质量为m的铁块以v2=1.0m/s从小车左端向右冲上小车,最终和小车共同运动.这个过程经历了t=1.8s,求该过程铁块相对于地面向右移动的最大距离.
质量为M=4m的小车以v1=0.50m/s沿光滑水平面向左运动.质量为m的铁块以v2=1.0m/s从小车左端向右冲上小车,最终和小车共同运动.这个过程经历了t=1.8s,求该过程铁块相对于地面向右移动的最大距离.
分析 M、m组成的系统动量守恒,应用动量守恒定律求出它们的共同速度,对m应用牛顿第二定律求出加速度,然后应用匀变速直线运动的速度位移公式求出位移.
解答 解:m、M所组成的系统动量守恒,取水平向左为正方向,由动量守恒定律得:
Mv1-mv2=(M+m)v共,
代入数据解得:v共=0.2m/s,
因v共方向水平向左,所以铁块的加速度为:$a=\frac{{{v_共}-(-{v_2})}}{t}=\frac{2}{3}m/s$
当铁块相对于地面速度为零时,铁块向右达到最大距离:$v_2^2=2a{s_m}$
最大位移:${s_m}=\frac{v_2^2}{2a}=0.75m$;
答:该过程铁块相对于地面向右移动的最大距离为0.75m.
点评 本题考查了求铁块的位移,分析清楚物体运动过程,应用动量守恒定律、牛顿第二定律与运动学公式即可解题,本题是一道力学综合题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
9.质量为m的物体从高h处自由落下(不计空气阻力),当它下落到高度为$\frac{3}{4}$h处时动能为( )
| A. | mgh | B. | $\frac{1}{4}$mgh | C. | $\frac{1}{2}$mgh | D. | $\frac{3}{4}$mgh |
6.能正确解释黑体辐射实验规律的是( )
| A. | 能量的经典连续理论 | |
| B. | 普朗克提出的能量量子化理论 | |
| C. | 牛顿提出的微粒说 | |
| D. | 以上三种理论体系任何一种都能解释 |
3.光电效应实验中,下列表述正确的是( )
| A. | 遏止电压与入射光的频率无关 | |
| B. | 入射光频率大于极限频率才能产生光电子 | |
| C. | 光照时间越长光电流越大 | |
| D. | 入射光足够强就可以有光电流 |
10.某金属在某一黄光照射下,刚好有光电子逸出,下列说法正确的是( )
| A. | 增大该黄光的光强,光电子的最大初动能将增加 | |
| B. | 用一束更强的红光代替黄光,也能发生光电效应 | |
| C. | 用紫光代替黄光,光电子的最大初动能将增加 | |
| D. | 对于某种金属存在一个“极限波长”,入射光的波长必须大于这个波长才能发生光电效应 |
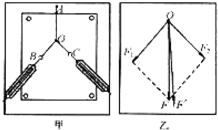 “验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
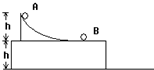 如图所示,水平地面上固定有高为h的平台,台面上有固定的光滑坡道,坡道顶端距台面高也为h,坡道底端与台面相切.小球A从坡道顶端由静止开始滑下,到达水平光滑的台面后与静止在台面上的小球B发生碰撞,并粘连在一起,共同沿台面滑行并从台面边缘飞出,落地点与飞出点的水平距离恰好为台高的一半.两球均可视为质点,忽略空气阻力,重力加速度为g.则,小球A刚滑至水平台面的速度vA=$\sqrt{2gh}$A、B两球的质量之比为mA:mB为1:3.
如图所示,水平地面上固定有高为h的平台,台面上有固定的光滑坡道,坡道顶端距台面高也为h,坡道底端与台面相切.小球A从坡道顶端由静止开始滑下,到达水平光滑的台面后与静止在台面上的小球B发生碰撞,并粘连在一起,共同沿台面滑行并从台面边缘飞出,落地点与飞出点的水平距离恰好为台高的一半.两球均可视为质点,忽略空气阻力,重力加速度为g.则,小球A刚滑至水平台面的速度vA=$\sqrt{2gh}$A、B两球的质量之比为mA:mB为1:3.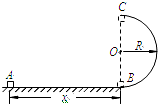 如图所示,水平光滑轨道AB与竖直半圆形光滑轨道在B点平滑连接,AB段长x=2.5m,半圆形轨道半径R=0.9m.质量m=0.10kg的小滑块(可视为质点)在水平恒力F作用下,从A点由静止开始运动,经B点时撤去力F,小滑块进入半圆形轨道,沿轨道恰好能运动到最高点C,然后从C点水平飞出.重力加速度g取10m/s2.求:
如图所示,水平光滑轨道AB与竖直半圆形光滑轨道在B点平滑连接,AB段长x=2.5m,半圆形轨道半径R=0.9m.质量m=0.10kg的小滑块(可视为质点)在水平恒力F作用下,从A点由静止开始运动,经B点时撤去力F,小滑块进入半圆形轨道,沿轨道恰好能运动到最高点C,然后从C点水平飞出.重力加速度g取10m/s2.求: