题目内容
长为L的轻杆一端安在光滑固定转动轴O上，另一端固定有一只质量为m的小球A（视为质点）。给小球一个初速度，使它在竖直面内绕O做圆周运动，已知：当小球到达最高点时，小球对杆的压力大小为小球重力的1/4；小球通过最低点时速度大小为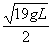
。求：
（1）小球通过最高点时的速率V。
（2）小球通过最低点时对杆的拉力大小F。
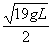。求：（1）小球通过最高点时的速率V。
（2）小球通过最低点时对杆的拉力大小F。
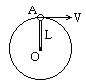
解：（1）小球在最高点的受力如图：小球在最高点的向心力由mg和N的合力来提供，由牛顿第二定律得
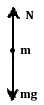
mg－N=m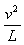
N=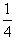
mg
解得：v=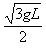
（2）小球在最低点时，杆对小球的拉力为F′，受力如图。同理由牛顿第二定律得：
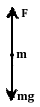
F′－mg=m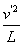
v'=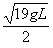
得：F′=5.75mg
由牛顿第三定律可知，小球对杆的拉力大小F=5.75mg
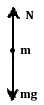
mg－N=m
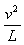
N=
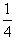mg 解得：v=
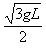
（2）小球在最低点时，杆对小球的拉力为F′，受力如图。同理由牛顿第二定律得：
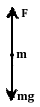
F′－mg=m
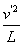
v'=
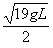
得：F′=5.75mg
由牛顿第三定律可知，小球对杆的拉力大小F=5.75mg
练习册系列答案
阅读快车系列答案
相关题目
