题目内容
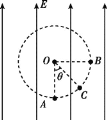
【题目】如图所示,在场强大小为E、方向竖直向上的匀强电场内取一个半径为R的圆周,圆周所在平面平行于电场方向,O点为该圆周的圆心,A点是圆周上的最低点,B点是圆周上最右侧的点.在A点有放射源,在圆周所在的平面内沿着垂直于电场向右的方向释放出相同的带正电的粒子,这些粒子从A点出发时的初速度大小各不相同,已知粒子的质量为m,电荷量为q,不计重力.
(1)某一粒子的运动轨迹经过圆周上的B点,求该粒子从A点出发时的初速度大小;
(2)取圆周上的某点C,设OC连线与OA夹角为θ,试写出粒子经过C点时的动能表达式;
【答案】(1)![]() (2)
(2)![]()
【解析】
由题中“在场强大小为E、方向竖直向上的匀强电场内取一个半径为R的圆周”可知,本题考查带电粒子在匀强电场中的运动,根据牛顿第二定律和动能定理可分析本题。
(1)粒子从A点到B点做类平抛运动,由牛顿第二定律得
![]()
水平方向上,有
![]()
竖直方向上,有
![]()
联立解得
![]() .
.
(2)粒子从A到C做类平抛运动,则
水平方向上,有
![]()
竖直方向上,有
![]()
得
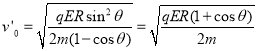
粒子从A点出发时的动能为
![]()
设经过C点时的动能为Ek,则有
![]()
解得
![]() .
.

练习册系列答案
相关题目