题目内容
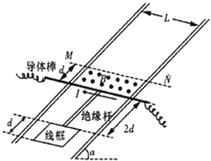
【题目】如图所示，两平行的光滑金属导轨安装在一倾角为α的光滑绝缘斜面上，导轨间距为L，电阻忽略不计且足够长，以宽度为d的有界匀强磁场垂直于斜面向上，磁感应强度为B．另有一长为2d的绝缘杆将一导体棒和一边长为d（d＜L）的正方形线框连在一起组成的固定装置，总质量为m，导体棒中通有大小恒为I的电流．将整个装置置于导轨上，开始时导体棒恰好位于磁场的下边界处．由静止释放后装置沿斜面向上运动，当线框的下边运动到磁场的上边界MN处时装置的速度恰好为零．重力加速度为g．
（1）求刚释放时装置加速度的大小；
（2）求这一过程中线框中产生的热量；
（3）之后装置将向下运动，然后再向上运动，经过若干次往返后，最终整个装置将在斜面上作稳定的往复运动．求稳定后装置运动的最高位置与最低位置之间的距离．
【答案】（1）
；（2）BILd－4mgdsinα；（3）
【解析】
试题分析：（1）刚释放时有BIL－ mgsinα=ma
解得 （3分）
（2）装置由静止释放到线框的下边运动到磁场的上边界MN过程中线框中产生的焦耳热为Q，由能量守恒
BIL·d－mgsinα·4d－Q=0
解得 Q=BILd－4mgdsinα （5分）
(3) 装置往复运动的最高位置：
线框的上边位于磁场的下边界，此时金属棒据磁场上边界为d； （3分）
装置往复运动到最低位置时：
金属棒在磁场内，设其距离上边界为x，则有
mgsinα·(x＋d)=BIL·x （3分）
解得 
（2分）
最高位置与最低位置之间的距离为
（2分）
练习册系列答案
相关题目
