题目内容
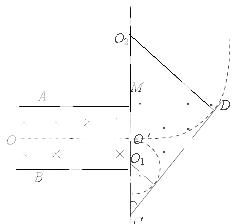
【题目】如图所示，两平行金属板AB中间有互相垂直的匀强电场和匀强磁场．A板带正电荷，B板带等量负电荷，电场强度为E；磁场方向垂直纸面向里，磁感应强度为B1 ． 平行金属板右侧有一挡板M，中间有小孔O′，OO′是平行于两金属板的中心线．挡板右侧有垂直纸面向外的匀强磁场，磁场应强度为B2 ． CD为磁场B2边界上的一绝缘板，它与M板的夹角θ=45°，O′C=a，现有大量质量均为m，含有各种不同电荷量、不同速度的带电粒子（不计重力），自O点沿OO′方向进入电磁场区域，其中有些粒子沿直线OO′方向运动，并进入匀强磁场B2中，求：
（1）进入匀强磁场B2的带电粒子的速度；
（2）能击中绝缘板CD的粒子中，所带电荷量的最大值；
（3）绝缘板CD上被带电粒子击中区域的长度．
【答案】
（1）解：沿直线OO′运动的带电粒子，设进入匀强磁场B2的带电粒子的速度为v，
根据B1qv=qE，
解得： 
答：进入匀强磁场B2的带电粒子的速度 
；
（2）解：粒子进入匀强磁场B2中做匀速圆周运动，
根据 
，
解得： 
因此，电荷量最大的带电粒子运动的轨道半径最小，
设最小半径为r1，此带电粒子运动轨迹与CD板相切，
则有：r1+ 
r1=a，
解得：r1=（ ﹣1）a．
电荷量最大值q=（ +1） 
．
答：能击中绝缘板CD的粒子中，所带电荷量的最大值 
；
（3）解：带负电的粒子在磁场B2中向上偏转，某带负电粒子轨迹与CD相切，设半径为r2，
依题意r2+a= r2
解得：r2=（ +1）a
则CD板上被带电粒子击中区域的长度为
X=r2﹣r1=2a
答：绝缘板CD上被带电粒子击中区域的长度2a．
【解析】（1）速度选择器的原理，电场力和洛伦兹力平衡，结合洛伦兹力公式，列式求解。
（2）带电粒子在磁场中运动的题目，首先确定圆心的位置，画出运动轨迹的图像，根据几何关系求出半径，根据带电粒子在磁场中运动时，洛伦兹力提供向心力烈式求解。
（3）根据几何关系，求出粒子半径，两半径之差，既为所求。
【考点精析】关于本题考查的洛伦兹力，需要了解洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功才能得出正确答案．
