题目内容
质量为m=50kg的人从质量为M=100kg的小船船头走到船尾．不计阻力，船长为L=6m，则人相对岸发生的位移为 ．船相对岸发生的位移为 ．
分析：人和小船组成的系统动量守恒，根据动量守恒定律求出船移动的位移大小．
解答：解：船和人组成的系统，在水平方向上动量守恒，人在船上行进，船向右退，有mv=MV．
人从船头走到船尾，设船后退的位移大小为x，则人相对于岸的位移大小为L-x．
由 m
=M
解得，x=
=
×6m=2m；
人相对于岸的位移大小为L-x=
=
×6m=4m
故答案为：4m，2m
人从船头走到船尾，设船后退的位移大小为x，则人相对于岸的位移大小为L-x．
由 m
| L-x |
| t |
| x |
| t |
解得，x=
| mL |
| M+m |
| 50 |
| 100+50 |
人相对于岸的位移大小为L-x=
| ML |
| M+m |
| 100 |
| 100+50 |
故答案为：4m，2m
点评：解决本题的关键掌握动量守恒定律的条件，以及知道在运用动量守恒定律时，速度必须相对于地面为参考系．
练习册系列答案
阅读快车系列答案
相关题目
（2012?桂林模拟）如图示为仓库中常用的皮带传输装置示意图，它由两台皮带传送机组成，一台水平传送，A、B 两端相距L1=3m，另一台倾斜，传送带与地面的倾角θ=37°，C、D 两端相距L2=2.8m，B、C相距很近．水平部分AB以υ1=5m/s的速率顺时针运转，倾斜部分CD以υ2=3m/s的速率顺时针运转．将质量为m=50kg 的一袋大米放在A 端，到达B 端后，速度大小不变地传到倾斜的CD 部分，米袋与传送带间的动摩擦因数均为0.5．求：米袋从A端到D 端所用的时间．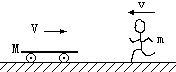
一辆小车在光滑的水平面上以V=1m/s的速度向右运动，小车的质量为M=100kg，如图所示．一质量为m=50kg的人从小车的右端迎面跳上小车，接触小车前的瞬间人的水平速度大小为v=5m/s．求：
摄制组在某大楼旁边拍摄武打片，要求特技演员从地面飞到屋顶．如图所示，导演在某房顶离地H=12m处架设了滑轮（人和车均视为质点，且滑轮直径远小于H），若轨道车从A处以v=10m/s的速度匀速运动到B处，绳BO与水平方向的夹角为53°．由于绕在滑轮上细钢丝的拉动，使质量为m=50kg的特技演员从地面由静止开始向上运动．在车从A运动到B的过程中（取g=10m/s2，sin53°=0.8，cos53°=0.6）（ ）| A、演员最大速度为6.0 m/s | B、演员上升高度为12 m | C、演员处于超重状态 | D、演员机械能增量为4275J |
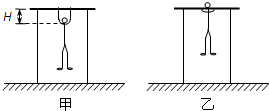“引体向上”是同学们常做的一项健身运动．如图甲所示，质量为m=50kg的某同学两手正握单杠，手臂完全伸直，身体呈自然悬垂状态，此时他的下颚距单杠的高度为H=0.4m，然后他用F=600N的恒力将身体向上拉至某位置时不再用力，身体依靠惯性继续向上运动，为保证其下颚超过单杠达到合格要求，如图乙所示．恒力F的作用时间至少为多少？不计空气阻力，取重力加速度g=10m/s2．