Question

【题目】如图所示，固定斜面C的倾角为θ，物体A放在斜面C上，物体B叠放在物体A上，A、B的质量均为m，且上、下表面均与斜面平行，A、B一起沿斜面匀速下滑，则（ ）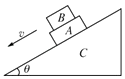

A.A与B之间没有静摩擦力
B.A受到B的静摩擦力方向沿斜面向上
C.A与B之间的动摩擦因数μ=tanθ
D.A受到斜面的滑动摩擦力大小为2mgsinθ

Answer 1

【答案】D
【解析】解：AB、对B受力分析可知，B受重力、支持力；将重力分解可知重力有沿斜面向下的分力，要使B能匀速下滑，受力一定平衡，故A对B应有沿斜面向上的摩擦力，由牛顿第三定律可知，A受到B的摩擦力应沿斜面向下，故AB错误；
C、A与B间的摩擦力为静摩擦力，无法根据滑动摩擦力的公式求解动摩擦因数，故C错误；
D、对AB整体分析，并将整体重力分解，可知沿斜面方向上，重力的分力与摩擦力等大反向，故A受的滑动摩擦力沿斜面向上，大小为2mgsinθ，故D正确．
故选：D．
【考点精析】本题主要考查了滑动摩擦力和静摩擦力的相关知识点，需要掌握滑动摩擦力:利用公式f=μF N 进行计算，其中FN 是物体的正压力，不一定等于物体的重力，甚至可能和重力无关.或者根据物体的运动状态，利用平衡条件或牛顿定律来求解；静摩擦力:静摩擦力大小可在0与fmax 之间变化，一般应根据物体的运动状态由平衡条件或牛顿定律来求解才能正确解答此题．