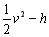题目内容
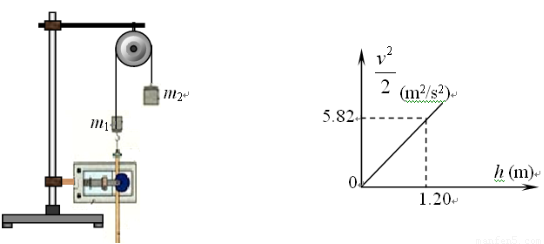
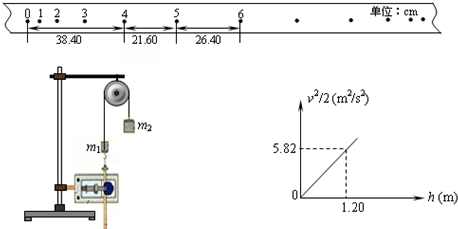
用如图实验装置验证m1、m2组成的系统机械能守恒.m2从高处由静止开始下落,m1上拖着的纸带打出一系列的点,对纸带上的点迹进行测量,即可验证机械能守恒定律.下图给出的是实验中获取的一条纸带:0是打下的第一个点,每相邻两计数点间还有4个点(图中未标出),计数点间的距离如图所示.已知m1=50g、m2=150g,则(g取10m/s2,结果保留两位有效数字)
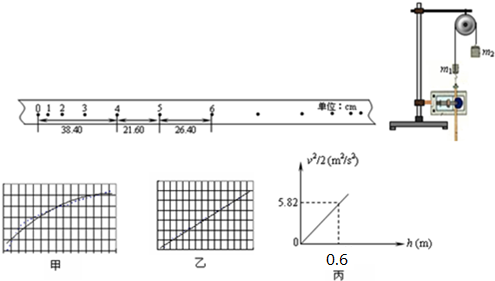
①在纸带上打下记数点5时的速度v=
②在打点0~5过程中系统动能的增量△EK=
③实验小组某同学先得出了v-h图象,继而又得出v2-h图象,如图甲、乙所示:该同学在得出v-h图象后,为什么还要作出v2-h图象?
④另一同学作出
v2-h图象如图丙,则当地的实际重力加速度g=

①在纸带上打下记数点5时的速度v=
2.4
2.4
m/s;②在打点0~5过程中系统动能的增量△EK=
0.58
0.58
J,系统势能的减少量△EP=0.60
0.60
J,由此得出的结论是在误差允许的范围内,m1、m2组成的系统机械能守恒
在误差允许的范围内,m1、m2组成的系统机械能守恒
;③实验小组某同学先得出了v-h图象,继而又得出v2-h图象,如图甲、乙所示:该同学在得出v-h图象后,为什么还要作出v2-h图象?
先作出的vB-h图象,不是一条直线,根据形状无法判断vB、h关系,进而考虑vB2-h图象,从而找出vB2、h之间的线性关系
先作出的vB-h图象,不是一条直线,根据形状无法判断vB、h关系,进而考虑vB2-h图象,从而找出vB2、h之间的线性关系
.④另一同学作出
| 1 | 2 |
9.7
9.7
m/s2.分析:①根据在匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度,可以求出打下记数点5时的速度大小;
②根据物体的初末动能大小可以求出动能的增加量,根据物体重力做功和重力势能之间的关系可以求出系统重力势能的减小量,比较动能增加量和重力势能减小量之间的关系可以得出机械能是否守恒;
③根据数学知识可知,得出图象若为直线,则可很容易的判断两个物理量之间的关系;
④根据图象的物理意义可知,图象的斜率大小等于物体的重力加速度大小.
②根据物体的初末动能大小可以求出动能的增加量,根据物体重力做功和重力势能之间的关系可以求出系统重力势能的减小量,比较动能增加量和重力势能减小量之间的关系可以得出机械能是否守恒;
③根据数学知识可知,得出图象若为直线,则可很容易的判断两个物理量之间的关系;
④根据图象的物理意义可知,图象的斜率大小等于物体的重力加速度大小.
解答:解:①根据在匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度,可知打第5个点时的速度为:
v5=
=
=2.4m/s
故答案为:2.4.
②物体的初速度为零,所以动能的增加量为:△Ek=
m
-0=0.58J;
重力势能的减小量等于物体重力做功,故:△EP=W=mgh=0.60J;
由此可知动能的增加量和势能的减小量基本相等,因此在在误差允许的范围内,m1、m2组成的系统机械能守恒.
故答案为:0.58,0.60,在误差允许的范围内,m1、m2组成的系统机械能守恒.
③根据数学知识可知,得出图象若为直线,则可很容易的判断两个物理量之间的关系.
故答案为:先作出的vB-h图象,不是一条直线,根据形状无法判断vB、h关系,进而考虑vB2-h图象,从而找出vB2、h之间的线性关系.
④本题中根据机械能守恒可知,mgh=
mv2,即有:
v2=gh,所以出
v2-h图象中图象的斜率表示重力加速度,由图可知,斜率k=9.7,故当地的实际重力加速度g=9.7m/s2.
故答案为:9.7.
v5=
| x46 |
| 2T |
| (21.60+26.40)cm |
| 2×0.1s |
故答案为:2.4.
②物体的初速度为零,所以动能的增加量为:△Ek=
| 1 |
| 2 |
| v | 2 5 |
重力势能的减小量等于物体重力做功,故:△EP=W=mgh=0.60J;
由此可知动能的增加量和势能的减小量基本相等,因此在在误差允许的范围内,m1、m2组成的系统机械能守恒.
故答案为:0.58,0.60,在误差允许的范围内,m1、m2组成的系统机械能守恒.
③根据数学知识可知,得出图象若为直线,则可很容易的判断两个物理量之间的关系.
故答案为:先作出的vB-h图象,不是一条直线,根据形状无法判断vB、h关系,进而考虑vB2-h图象,从而找出vB2、h之间的线性关系.
④本题中根据机械能守恒可知,mgh=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:9.7.
点评:本题全面的考查了验证机械能守恒定律中的数据处理问题,要熟练掌握匀变速直线运动的规律以及功能关系,增强数据处理能力.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目

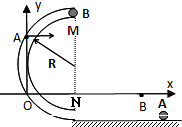 用如图实验装置验证机械能守恒定律.通过电磁铁控制的小铁球从A点自由下落,下落过程中经过光电门B时,通过与之相连的毫秒计时器(图中未画出)记录下挡光时间t,测出AB之间的距离h.实验前应调整光电门位置使小球下落过程中球心通过光电门中的激光束.
用如图实验装置验证机械能守恒定律.通过电磁铁控制的小铁球从A点自由下落,下落过程中经过光电门B时,通过与之相连的毫秒计时器(图中未画出)记录下挡光时间t,测出AB之间的距离h.实验前应调整光电门位置使小球下落过程中球心通过光电门中的激光束.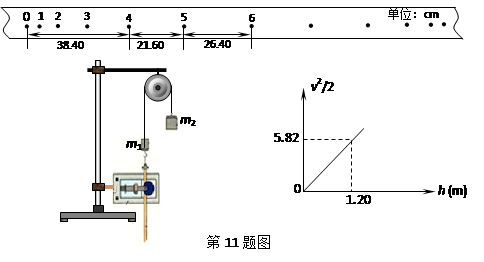
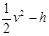 图象如图,则当地的实际重力加速度g = m/s2.
图象如图,则当地的实际重力加速度g = m/s2.