题目内容
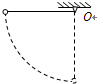 如图所示,用轻绳悬挂一小球,将小球拉至绳水平位置,然后由静止释放,让其自由下摆.在小球摆向最低点的过程中,下列说法正确的是( )
如图所示,用轻绳悬挂一小球,将小球拉至绳水平位置,然后由静止释放,让其自由下摆.在小球摆向最低点的过程中,下列说法正确的是( )分析:小球被释放后做圆周运动,只有重力做功,机械能守恒,运动过程中,小球具有向心加速度和切向加速度,根据牛顿第二定律列式判断拉力T的变化情况.
解答:解:A、小球的速度增大,在最低点竖直分速度为零,可知竖直分速度先增大后减小,根据P=mgvy可知,重力的功率先增大,后减小,故A正确;
B、从最高点到最低点的过程中,根据动能定理得:
mv2=mgl
在最低点有:
T-mg=m
解得:T=3mg,与l无关,故B正确;
C、悬绳变长后,水平方向的运动情况没有发生改变,则平均速度也没有发生改变,所以时间变长了,故C正确;
D、小球做的是变加速圆周运动,合力不指向圆心,故D错误.
故选ABC
B、从最高点到最低点的过程中,根据动能定理得:
| 1 |
| 2 |
在最低点有:
T-mg=m
| v2 |
| l |
解得:T=3mg,与l无关,故B正确;
C、悬绳变长后,水平方向的运动情况没有发生改变,则平均速度也没有发生改变,所以时间变长了,故C正确;
D、小球做的是变加速圆周运动,合力不指向圆心,故D错误.
故选ABC
点评:本题主要考查了圆周运动向心力公式、机械能守恒定律及牛顿第二定律的直接应用,要求同学们能正确分析小球的受力情况,会利用特殊点解题,难度适中.

练习册系列答案
相关题目
如图所示,用轻绳悬挂一质量为m的小球,对小球再施加一个力,使绳与竖直方向成β角并绷紧,小球处于静止状态,此力最小值为( )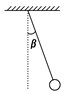
| A.mgcosβ | B.mgsinβ |
| C.mgtanβ | D.mgcotβ |
 如图所示,用轻绳AC和BC悬挂一重物,绳与水平天花板的夹角分别为60°和30°,已知C下面吊的重物100N.求绳 AC和BC的拉力.
如图所示,用轻绳AC和BC悬挂一重物,绳与水平天花板的夹角分别为60°和30°,已知C下面吊的重物100N.求绳 AC和BC的拉力. 如图所示,用轻绳AO和OB将重为G的重物悬挂在水平天花板和竖直墙壁之间处于静止状态,AO绳水平,OB绳与竖直方向的夹角为θ.设AO绳的拉力大小为T1、OB绳的拉力大小为T2,下列判断正确的是( )
如图所示,用轻绳AO和OB将重为G的重物悬挂在水平天花板和竖直墙壁之间处于静止状态,AO绳水平,OB绳与竖直方向的夹角为θ.设AO绳的拉力大小为T1、OB绳的拉力大小为T2,下列判断正确的是( )