题目内容
【题目】为了使粒子经过一系列的运动后，又以原来的速率沿相反方向回到原位，可设计如下的一个电磁场区域（如图所示）：水平线QC以下是水平向左的匀强电场，区域Ⅰ(梯形PQCD)内有垂直纸面向里的匀强磁场，磁感应强度为B；区域Ⅱ(三角形APD)内的磁场方向与Ⅰ内相同，但是大小可以不同，区域Ⅲ(虚线PD之上、三角形APD以外)的磁场与Ⅱ内大小相等、方向相反．已知等边三角形AQC的边长为2l，P、D分别为AQ、AC的中点．带正电的粒子从Q点正下方、距离Q点为l的O点以某一速度射出，在电场力作用下从QC边中点N以速度v0垂直QC射入区域Ⅰ，再从P点垂直AQ射入区域Ⅲ，又经历一系列运动后返回O点．（粒子重力忽略不计）求：
（1）该粒子的比荷．
（2）粒子从O点出发再回到O点的整个运动过程所需时间．
【答案】(1) 
(2) 
或 
【解析】试题分析：本题属于带电粒子在组合场中运动问题，磁场中圆周运动要画轨迹分析运动过程，探索规律，寻找半径与三角形边的关系是关键．
（1）从N到P，做匀速圆周运动，根据牛顿第二定律和洛仑兹力表达式有：
根据题意有R＝l 解得： 
（2）粒子从O到N与从N到O是逆过程，N到O做类平抛运动，在区域Ⅰ、区域Ⅱ和Ⅲ中都做匀速圆周运动．带电粒子在电磁场中运动的总时间包括三段：电场中往返的时间t0、区域Ⅰ中的时间t1、区域Ⅱ和Ⅲ中的时间t2＋t3
根据平抛运动规律有
粒子在区域Ⅰ中运动时，由线速度和角速度关系得：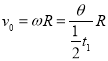 
即
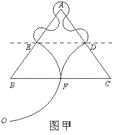
①若粒子在区域Ⅱ和Ⅲ内的运动如图甲所示，则总路程为
个圆周，根据几何关系有
AE＝(4nr + r)＝l 解得： r＝l/(4n + 1) 其中n＝0，1，2……
区域Ⅱ和Ⅲ内总路程为
总时间
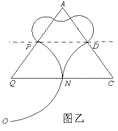
②若粒子在区域Ⅱ和Ⅲ内运动如图乙所示，则总路程为
个圆周，根据几何关系有：
AP＝(4nr +3r)＝l 解得： r＝ l/(4n + 3) 其中n＝0，1，2……
区域Ⅱ和Ⅲ内总路程为
总时间
