题目内容
木块质量为1kg,放在有摩擦的水平地面上,在12N水平拉力作用下,从静止开始做匀加速直线运动,经4s后位移为24m,求:
(1)木块的加速度多大?所受摩擦力多大?
(2)如果木块从静止开始运动5s后撤去12N的拉力,同时另加一个水平阻力,木块继续前进5m停止,那么所加阻力多大?
(1)木块的加速度多大?所受摩擦力多大?
(2)如果木块从静止开始运动5s后撤去12N的拉力,同时另加一个水平阻力,木块继续前进5m停止,那么所加阻力多大?
分析:(1)根据匀变速直线运动的位移时间公式求出木块的加速度,结合牛顿第二定律求出摩擦力的大小.
(2)根据速度位移公式求出木块减速运动的加速度,结合牛顿第二定律求出所加的阻力大小.
(2)根据速度位移公式求出木块减速运动的加速度,结合牛顿第二定律求出所加的阻力大小.
解答:解:(1)根据位移时间公式x=
at2得:
a=
=
m/s2=3m/s2.
根据牛顿第二定律得:
F-f=ma
解得:f=F-ma=12-1×3N=9N.
(2)5s后的速度为:v=at=3×5m/s=15m/s.
根据速度位移公式得:v2=2a′x′
解得减速运动加速度的大小为:a′=
=
m/s2=22.5m/s2.
根据牛顿第二定律得:f′+f=ma′
解得:f′=ma′-f=22.5-9=13.5N
答:(1)木块的加速度为3m/s2,所受的摩擦力为9N.
(2)所加阻力为13.5N.
| 1 |
| 2 |
a=
| 2x |
| t2 |
| 48 |
| 16 |
根据牛顿第二定律得:
F-f=ma
解得:f=F-ma=12-1×3N=9N.
(2)5s后的速度为:v=at=3×5m/s=15m/s.
根据速度位移公式得:v2=2a′x′
解得减速运动加速度的大小为:a′=
| v2 |
| 2x′ |
| 225 |
| 2×5 |
根据牛顿第二定律得:f′+f=ma′
解得:f′=ma′-f=22.5-9=13.5N
答:(1)木块的加速度为3m/s2,所受的摩擦力为9N.
(2)所加阻力为13.5N.
点评:本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 (1)发电站通过升压变压器、输电导线、降压变压器把电能输送到用户,如果升压变压器和降压变压器都可视为理想变压器,当发电机的输出功率为100kW,输出电压为250V,升压变压器的原副线圈匝数比为1:25,求升压变压器的输出电压和输电导线上的电流.
(1)发电站通过升压变压器、输电导线、降压变压器把电能输送到用户,如果升压变压器和降压变压器都可视为理想变压器,当发电机的输出功率为100kW,输出电压为250V,升压变压器的原副线圈匝数比为1:25,求升压变压器的输出电压和输电导线上的电流. 如图所示,在水平地面上放一质量为1kg的木块,木块与地面间的动摩擦因数为0.6,在水平方向上对木块同时施加相互垂直的两个拉力F1、F2,已知F1=3N,F2=4N,设最大静摩擦力等于滑动摩擦力,g取10N/kg,则
如图所示,在水平地面上放一质量为1kg的木块,木块与地面间的动摩擦因数为0.6,在水平方向上对木块同时施加相互垂直的两个拉力F1、F2,已知F1=3N,F2=4N,设最大静摩擦力等于滑动摩擦力,g取10N/kg,则 如图所示,质量为4kg的平板小车静止在光滑的水平地面上.小车左端放一质量为1kg的木块,车的右端固定一个轻质弹簧,现给木块一个水平向右10N?s的瞬时冲量,木块便沿车板向右滑行,在与弹簧相碰后又沿原路返回,并且恰好能到达小车的左端,求:
如图所示,质量为4kg的平板小车静止在光滑的水平地面上.小车左端放一质量为1kg的木块,车的右端固定一个轻质弹簧,现给木块一个水平向右10N?s的瞬时冲量,木块便沿车板向右滑行,在与弹簧相碰后又沿原路返回,并且恰好能到达小车的左端,求: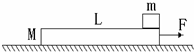 如图所示,木板静止于水平地面上,在其最右端放一可视为质点的木块.已知木块的质量m=1kg,木板的质量M=4kg,长L=2.5m,上表面光滑,下表面与地面之间的动摩擦因数μ=0.2.现用水平恒力F=20N拉木板,g取10m/s2,求:
如图所示,木板静止于水平地面上,在其最右端放一可视为质点的木块.已知木块的质量m=1kg,木板的质量M=4kg,长L=2.5m,上表面光滑,下表面与地面之间的动摩擦因数μ=0.2.现用水平恒力F=20N拉木板,g取10m/s2,求: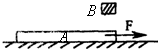 如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.若要使木块不从木板上滑下来,求木板的最小长度.
如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.若要使木块不从木板上滑下来,求木板的最小长度.