题目内容
18. 如图,带等量异种电荷的平行金属板,其间距离为d,两板间的电势差为U,极板与水平方向成30°角放置,有一质量为m、速率为v0的带电小球恰好沿水平方向穿过极板间的匀强电场区域,求:
如图,带等量异种电荷的平行金属板,其间距离为d,两板间的电势差为U,极板与水平方向成30°角放置,有一质量为m、速率为v0的带电小球恰好沿水平方向穿过极板间的匀强电场区域,求:(1)小球带何种电荷?电荷量是多少?
(2)小球的加速度
(3)小球穿过极板时的速率.
分析 (1)根据小球的运动状态判断小球所受电场力的方向,然后判断小球的电性;在竖直方向应用平衡条件求出电荷量;
(2)根据小球的受力情况应用牛顿第二定律求出小球的加速度;
(3)应用匀变速直线运动的速度位移公式求出小球的速度.
解答 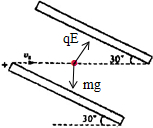 解:(1)小球沿水平方向做直线运动,则小球受到垂直于极板斜向右上方的电场力,
解:(1)小球沿水平方向做直线运动,则小球受到垂直于极板斜向右上方的电场力,
电场力方向与场强方向相同,则小球带正电;小球沿水平方向做直线运动,
小球在竖直方向所受合力为零,在竖直方向,由平衡条件得:
mg=q$\frac{U}{d}$cos30°,
解得:q=$\frac{2\sqrt{3}mgd}{3U}$;
(2)在水平方向,由牛顿第二定律得:mgtan30°=ma,
解得:a=$\frac{\sqrt{3}}{3}$g;
(3)小球在水平方向做匀加速直线运动,由匀变速直线运动的速度位移公式得:
v=$\sqrt{{v}_{0}^{2}+2a\frac{d}{sin30°}}$=$\sqrt{{v}_{0}^{2}+\frac{4\sqrt{3}gd}{3}}$;
答:(1)小球带正电荷,电荷量是$\frac{2\sqrt{3}mgd}{3U}$;
(2)小球的加速度大小为$\frac{\sqrt{3}}{3}$g,方向水平向右;
(3)小球穿过极板时的速率为$\sqrt{{v}_{0}^{2}+\frac{4\sqrt{3}gd}{3}}$.
点评 本题考查了判断小球的电性、求电荷量、加速度与速率问题,知道小球做直线运动的条件是解题的关键;应用运动的合成与分解、平衡条件、牛顿第二定律与运动学公式可以解题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
8. 叠罗汉是一种二人以上层层叠成各种造型的游戏娱乐形式,也是一种高难度的杂技,图示为六人叠成的三层静态造型,假设每个人的重量均为G,下面五人的背部都均呈水平状态,他们站在质量不计的水平木板上,木板下面用轻质量弹簧支撑,初始时系统保持静止状态则( )
叠罗汉是一种二人以上层层叠成各种造型的游戏娱乐形式,也是一种高难度的杂技,图示为六人叠成的三层静态造型,假设每个人的重量均为G,下面五人的背部都均呈水平状态,他们站在质量不计的水平木板上,木板下面用轻质量弹簧支撑,初始时系统保持静止状态则( )
 叠罗汉是一种二人以上层层叠成各种造型的游戏娱乐形式,也是一种高难度的杂技,图示为六人叠成的三层静态造型,假设每个人的重量均为G,下面五人的背部都均呈水平状态,他们站在质量不计的水平木板上,木板下面用轻质量弹簧支撑,初始时系统保持静止状态则( )
叠罗汉是一种二人以上层层叠成各种造型的游戏娱乐形式,也是一种高难度的杂技,图示为六人叠成的三层静态造型,假设每个人的重量均为G,下面五人的背部都均呈水平状态,他们站在质量不计的水平木板上,木板下面用轻质量弹簧支撑,初始时系统保持静止状态则( )| A. | 最底层正中间的人的一只脚对水平长木板的压力为$\frac{7}{4}$G | |
| B. | 最底层中间的人的一只脚对水平长木板的压力为$\frac{5}{4}$G | |
| C. | 最顶层人武初速度离开一瞬间,中间层左侧的人的一只脚收到的支持力为$\frac{3}{5}$G | |
| D. | 最顶层人武初速度离开一瞬间,中间层左侧的人的一只脚收到的支持力为$\frac{1}{2}$G |
6.关于电动势下列说法正确的是( )
| A. | 电源电动势等于电源正负极之间的电势差 | |
| B. | 电源电动势总等于内、外电路上的电压之和,所以它的数值与外电路的组成有关 | |
| C. | 干电池电动势为1.5V,表明将1C的正电荷从电源负极移到正极,通过非静电力做功,将其它形式的能量1.5J转化为电能 | |
| D. | 电源的电动势跟电源内静电力做的功成正比,跟通过的电荷量成反比 |
13.下列说法中正确的是( )
| A. | 布朗运动的剧烈程度与温度有关,所以布朗运动也叫做热运动 | |
| B. | 彩色液晶显示屏是应用液晶在不同电场中对不同颜色的光吸收强度不同制成的 | |
| C. | 能量耗散说明能量在不断减少 | |
| D. | 热力学第二定律也可以表述为:气体向真空的自由膨胀是不可逆的 |
3.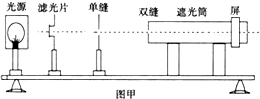 在“用双缝干涉测量光的波长”实验中,实验装置如图所示.以线状白炽灯为光源,对实验装置进行了调节并观察实验现象后,总结出以下几点,其中你认为正确的是( )
在“用双缝干涉测量光的波长”实验中,实验装置如图所示.以线状白炽灯为光源,对实验装置进行了调节并观察实验现象后,总结出以下几点,其中你认为正确的是( )
 在“用双缝干涉测量光的波长”实验中,实验装置如图所示.以线状白炽灯为光源,对实验装置进行了调节并观察实验现象后,总结出以下几点,其中你认为正确的是( )
在“用双缝干涉测量光的波长”实验中,实验装置如图所示.以线状白炽灯为光源,对实验装置进行了调节并观察实验现象后,总结出以下几点,其中你认为正确的是( )| A. | 单缝及双缝必须平行放置 | B. | 干涉条纹与双缝垂直 | ||
| C. | 干涉条纹疏密程度与双缝间距有关 | D. | 干涉条纹间距与光的波长有关 |
7.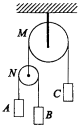 如图所示,M为定滑轮,一根细绳跨过M,一端系着物体C,另一端系着一动滑轮N,动滑轮N两侧分别悬挂着A、B两物体,已知B物体的质量为3kg,不计滑轮和绳的质量以及一切摩擦,若C物体的质量为9kg,则关于C物体的状态下列说法正确的是( )
如图所示,M为定滑轮,一根细绳跨过M,一端系着物体C,另一端系着一动滑轮N,动滑轮N两侧分别悬挂着A、B两物体,已知B物体的质量为3kg,不计滑轮和绳的质量以及一切摩擦,若C物体的质量为9kg,则关于C物体的状态下列说法正确的是( )
 如图所示,M为定滑轮,一根细绳跨过M,一端系着物体C,另一端系着一动滑轮N,动滑轮N两侧分别悬挂着A、B两物体,已知B物体的质量为3kg,不计滑轮和绳的质量以及一切摩擦,若C物体的质量为9kg,则关于C物体的状态下列说法正确的是( )
如图所示,M为定滑轮,一根细绳跨过M,一端系着物体C,另一端系着一动滑轮N,动滑轮N两侧分别悬挂着A、B两物体,已知B物体的质量为3kg,不计滑轮和绳的质量以及一切摩擦,若C物体的质量为9kg,则关于C物体的状态下列说法正确的是( )| A. | 当A的质量取值合适,C物体有可能处于平衡状态 | |
| B. | 无论A物体的质量是多大,C物体不可能平衡 | |
| C. | 当A的质量足够大时,C物体不可能向上加速运动 | |
| D. | 当A的质量取值合适,C物体可以向上加速也可以向下加速运动 |
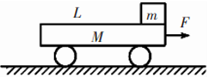 如图所示,平板小车静止于水平地面上,在其最右端放一可视为质点的小木块,已知木块的质量m=1kg,小车的质量M=4kg,上表面与木块间滑动摩擦因数μ=0.3,地面给小车的阻力与地面所受正压力成正比,比值为λ=0.2,现用向右的水平恒力F=30N拉平板小车,该水平恒力F作用的时间t1=2s,g取10m/s2.
如图所示,平板小车静止于水平地面上,在其最右端放一可视为质点的小木块,已知木块的质量m=1kg,小车的质量M=4kg,上表面与木块间滑动摩擦因数μ=0.3,地面给小车的阻力与地面所受正压力成正比,比值为λ=0.2,现用向右的水平恒力F=30N拉平板小车,该水平恒力F作用的时间t1=2s,g取10m/s2.