��Ŀ����
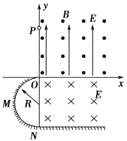
����Ŀ����ֱ��Ϊd��Բ�������ڴ�������ǿ�ų����Ÿ�Ӧǿ��ΪB���ų�����ֱ��Բ��ָ��ֽ�⣮һ�����Ϊq������Ϊm�Ĵ��������ӣ��Ӵų������һ��ֱ��AC�ϵ�A����ֽ������ų������ٶȷ�����AC������15��ǣ���ͼ��ʾ�����������ڴų������˶��Ĺ����У��ٶȵķ���һ���ı���90��.�����ɺ��Բ��ƣ���
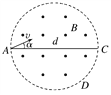
(1)�������ڴų��������˶����õ�ʱ��t��
(2)����������ʱ���ٶȴ�Сv.
���𰸡�(1)![]() ��(2)
��(2)![]()
������������������������Ӵ�ֱ������ǿ�ų��У������������ṩ���������������ۣ��������ӵĹ켣����Ӧ��Բ�Ľǵ����ٶȵ�ƫ��ǣ�������֪�켣����Ӧ��Բ�Ľ���90�㣬��������������ڴų��������˶����õ�ʱ��t�������켣���ɼ���֪ʶ�������Բ���˶��İ뾶���ɰ뾶��ʽ�������������ʱ���ٶȴ�Сv.
��1���������Ӵ�ֱ������ǿ�ų���������Բ���˶�ʱ���켣����Ӧ��Բ�Ľǵ����ٶȵ�ƫ��ǣ����⣬�����ٶȵķ���һ���ı���90�㣮��֪�켣����Ӧ��Բ�Ľ���90�㣬������
�ڴų��������˶����õ�ʱ��![]() , ���������ṩ���������У�
, ���������ṩ���������У� ![]() ����ã�
����ã� ![]() ������
������ ![]() ��
��
��2�����������˶��Ĺ켣����ͼ�����������Բ���˶��İ뾶Ϊr�����ɼ���֪ʶ��
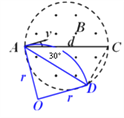
![]() �����
����� ![]() ,��
,��![]() ��
��![]() ��
��