题目内容
12.如图甲所示,在真空中足够大的绝缘水平地面上,一个质量为m=0.2kg、带电荷量为q=+2.0×10-6C的小物块处于静止状态,小物块与地面间的动摩擦因数μ=0.1.从t=0时刻开始,空间加上一个如图乙所示的场强大小和方向呈周期性变化的电场(取水平向右的方向为正方向,g取10m/s2)求:
(1)前17秒内小物块的位移大小;
(2)前17秒内电场力对小物块做的功.
分析 (1)根据牛顿第二定律求出物块在0~2s内和2~4s内的加速度,利用运动学公式求出0~2s内和2~4s内的位移,及第2s末和第4s末的速度,得到小物块做周期为4s的匀加速和匀减速运动.分别求出前16s物块的位移和第17s内的位移,再求总位移.
(2)根据动能定理求电场力对小物块所做的功
解答 解:(1)0-2秒内物块加速度为:
${a_1}=\frac{{q{E_1}-μmg}}{m}=2m/{s^2}$
位移为:${s_1}=\frac{1}{2}{a_1}{t_1}^2=4m$
2s末的速度为:v2=a1t1=4m/s
2-4秒内物块加速度为:${a_2}=\frac{{-q{E_2}-μmg}}{m}=-2m/{s^2}$
位移s2=s1=4m4s末的速度v4=0
因此小物块做周期为4s的加速和减速运动,前17s的位移为4个周期的位移加上第17s内的位移为:${s_{17}}=\frac{1}{2}{a_1}{t^2}=1m$
前17s的位移为:s=4(s1+s2)+s17=33m
(2)第17s末的速度为:v17=a1t1=1m/s
由动能定理得:$\frac{1}{2}m{v_{17}}^2-0={w_电}-μmgs$
代入数据得17s内电场力做功为w电=6.7J
答:(1)前17秒内小物块的位移大小为33m;
(2)前17秒内电场力对小物块做的功为6.7J.
点评 本题是物块在周期性的电场力作用下运动的问题,要抓住规律,也可以作速度-时间图象分析求解

练习册系列答案
相关题目
20. 如图所示,圆弧形桥面半径L,汽车以一定的速度V (V<$\sqrt{gL}$)经过桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )
如图所示,圆弧形桥面半径L,汽车以一定的速度V (V<$\sqrt{gL}$)经过桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )
 如图所示,圆弧形桥面半径L,汽车以一定的速度V (V<$\sqrt{gL}$)经过桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )
如图所示,圆弧形桥面半径L,汽车以一定的速度V (V<$\sqrt{gL}$)经过桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )| A. | 在竖直方向汽车受到三个力:重力和桥面的支持力和向心力 | |
| B. | 在竖直方向汽车只受两个力,重力和桥面的支持力 | |
| C. | 汽车对桥面的压力小于汽车的重力 | |
| D. | 汽车对桥面的压力大于汽车的重力 |
7. 如图所示,虚线是两个等量点电荷所产生的静电场中的一簇等势线,一不计重力的带电粒子从a点射入电场后恰能沿图中的实线运动,b点是其运动轨迹上的另一点,则下述判断正确的是( )
如图所示,虚线是两个等量点电荷所产生的静电场中的一簇等势线,一不计重力的带电粒子从a点射入电场后恰能沿图中的实线运动,b点是其运动轨迹上的另一点,则下述判断正确的是( )
 如图所示,虚线是两个等量点电荷所产生的静电场中的一簇等势线,一不计重力的带电粒子从a点射入电场后恰能沿图中的实线运动,b点是其运动轨迹上的另一点,则下述判断正确的是( )
如图所示,虚线是两个等量点电荷所产生的静电场中的一簇等势线,一不计重力的带电粒子从a点射入电场后恰能沿图中的实线运动,b点是其运动轨迹上的另一点,则下述判断正确的是( )| A. | 若粒子带正电,两等量点电荷均带正电 | |
| B. | 若粒子带负电,a点电势低于b点电势 | |
| C. | 由a到b的过程中电场力对带电粒子做负功 | |
| D. | 由a到b的过程中带电粒子的动能增大 |
4.甲、乙两物体从同一位置处相隔0.5s先后以同一加速度从静止出发,则在以后的运动过程中( )
| A. | 两物体速度差不变 | |
| B. | 两物体速度差越来越大 | |
| C. | 两物体距离越来越大 | |
| D. | 甲物体相对于乙物体做匀速直线运动 |
1.将水平弹簧振子从其平衡位置O拉开到位置A然后自由释放.若OA距离增大,则下列判断中正确的是( )
| A. | 振动的位移要大些 | B. | 振动的周期要长些 | ||
| C. | 振动的频率要大些 | D. | 振动的能量要大些 |
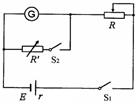 将满偏电流Ig=300μA、内阻未知的电流表G改装成电压表并进行核对.
将满偏电流Ig=300μA、内阻未知的电流表G改装成电压表并进行核对.