题目内容
9.两个质量不同的人造卫星在同一圆周轨道上一前一后绕地球做匀速圆周运动,则它们一定具有相同的( )| A. | 周期 | B. | 速度 | C. | 加速度 | D. | 向心力 |
分析 根据人造卫星的万有引力等于向心力,列式求出线速度、角速度、和向心力的表达式进行讨论即可.
注意矢量的方向性.
解答 解:卫星做圆周运动,由万有引力提供向心力,则有:
F=$\frac{GMm}{{r}^{2}}$=ma=m$\frac{{4π}^{2}}{{T}^{2}}$r=m$\frac{{v}^{2}}{r}$
A、T=2π $\sqrt{\frac{{r}^{3}}{GM}}$,两个质量不同的人造卫星在同一圆周轨道上一前一后绕地球做匀速圆周运动,所以它们一定具有相同的周期,故A正确;
B、v=$\sqrt{\frac{GM}{r}}$,它们一定具有相同的速度大小,方向不同,故B错误;
C、a=$\frac{GM}{{r}^{2}}$,它们一定具有相同的加速度大小,方向不同,故C错误;
D、F=$\frac{GMm}{{r}^{2}}$,它们一定具有相同的向心力大小,方向不同,故D错误;
故选:A.
点评 本题关键抓住万有引力提供向心力,先列式求解出线速度和角速度的表达式,再进行讨论,知道矢量相同必须是大小、方向都相同.

练习册系列答案
相关题目
20.物理兴趣小组利用图甲中的器材进行如下实验:
第一步:按图(甲)所示的电路图接好电路.
第二步:把电键S打到1,移动滑动变阻器的滑片,测得多组电压表和电流表的读数如表.
第三步:按电键S打到2,移动滑动变阻器的滑片,测得多组电压表和电流表的读数并在图(乙)中画出相应的图象如图所示.
第四步:理整仪器.
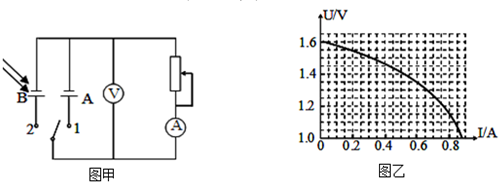
完成下列问题:
(1)在图(乙)中作出第二步实验的U-I图象,求出干电池A的电动势EA=1.52V,内电阻r=0.70Ω.
(2)在第二步中当滑动变阻器的电阻为某值时,电压表读数为1.2V,保持滑动变阻器的阻值不变把电键S打到2,则此时硅光电池B的输出功率P=0.73W.
第一步:按图(甲)所示的电路图接好电路.
第二步:把电键S打到1,移动滑动变阻器的滑片,测得多组电压表和电流表的读数如表.
| U/V | 1.42 | 1.38 | 1.32 | 1.35 | 1.18 | 1.10 |
| I/A | 0.15 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
第四步:理整仪器.

完成下列问题:
(1)在图(乙)中作出第二步实验的U-I图象,求出干电池A的电动势EA=1.52V,内电阻r=0.70Ω.
(2)在第二步中当滑动变阻器的电阻为某值时,电压表读数为1.2V,保持滑动变阻器的阻值不变把电键S打到2,则此时硅光电池B的输出功率P=0.73W.
17.下列单位属于国际单位制中基本单位的是( )
| A. | 千克 | B. | 厘米 | C. | 米/秒 | D. | 牛顿 |
1. 某种气体在不同温度下的气体分子速率分布曲线如图所示,图中f(v)表示v处单位速率区间内的分子数百分率,所对应的温度分别为TⅠ、TⅡ、TⅢ则( )
某种气体在不同温度下的气体分子速率分布曲线如图所示,图中f(v)表示v处单位速率区间内的分子数百分率,所对应的温度分别为TⅠ、TⅡ、TⅢ则( )
 某种气体在不同温度下的气体分子速率分布曲线如图所示,图中f(v)表示v处单位速率区间内的分子数百分率,所对应的温度分别为TⅠ、TⅡ、TⅢ则( )
某种气体在不同温度下的气体分子速率分布曲线如图所示,图中f(v)表示v处单位速率区间内的分子数百分率,所对应的温度分别为TⅠ、TⅡ、TⅢ则( )| A. | TⅠ>TⅡ>TⅢ | B. | TⅢ>TⅡ>TⅠ | C. | TⅡ>TⅠ,TⅡ>TⅢ | D. | TⅠ=TⅡ=TⅢ |
18.火星和木星沿着各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知( )
| A. | 火星和木星公转周期相等 | |
| B. | 火星和木星绕太阳运行速度的大小始终相等 | |
| C. | 火星和木星公转周期之比的平方等于它们轨道半长轴之比的立方 | |
| D. | 相同时间内,火星与太阳连线扫过的面积等与木星与太阳连线扫过的面积 |
19.在力学理论建立的过程中,有许多伟大的科学家做出了贡献,下列有关科学家和他们的贡献说法正确的是( )
| A. | 卡文迪许通过实验测出了引力常量G | |
| B. | 牛顿用实验直接验证了惯性定律 | |
| C. | 伽利略通过斜面实验合理外推解释了自由落体运动是匀变速直线运动 | |
| D. | 开普勒发现了行星运动的规律 |
 如图所示,在“探究功与物体速度变化的关系”的实验中:
如图所示,在“探究功与物体速度变化的关系”的实验中: 如图所示,在游乐场中,有一种大型游戏机械叫“跳楼机”.参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面124m的高处,然后由静止释放.为研究方便,可以认为座椅沿轨道做自由落体运动3s后,开始受到恒力制动,做匀减速运动,且下落到离地面4m高处时速度刚好减小到零.然后再让座椅以相当缓慢的速度稳稳落下,将游客送回地面,取g=10m/s2.求:
如图所示,在游乐场中,有一种大型游戏机械叫“跳楼机”.参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面124m的高处,然后由静止释放.为研究方便,可以认为座椅沿轨道做自由落体运动3s后,开始受到恒力制动,做匀减速运动,且下落到离地面4m高处时速度刚好减小到零.然后再让座椅以相当缓慢的速度稳稳落下,将游客送回地面,取g=10m/s2.求: 如图所示,竖直平面内的轨道由足够长的光滑斜面轨道AB和半径为R的光滑半圆形轨道BD连接而成,B为半圆形轨道的最低点,D为半圆形轨道的最高点,重力加速度为g,让质量为m的小球从斜面上某点由静止开始释放:
如图所示,竖直平面内的轨道由足够长的光滑斜面轨道AB和半径为R的光滑半圆形轨道BD连接而成,B为半圆形轨道的最低点,D为半圆形轨道的最高点,重力加速度为g,让质量为m的小球从斜面上某点由静止开始释放: