题目内容
1.一质点沿直线Ox方向做减速直线运动,它离开O点的距离x随时间变化的关系为x=(6t-2t3)m,它的速度v随时间t变化的关系为v=(6-6t2)m/s,则该质点从t=0到t=2s间的平均速度、平均速率分别为( )| A. | -2m/s、6m/s | B. | -2m/s、2m/s | C. | -2m/s、-18m/s | D. | 6m/s、6m/s |
分析 平均速度等于位移与时间的比值,平均速率等于路程与时间的比值,根据位移表达式和速度表达式求出2s内的位移和路程,从而求出平均速度和平均速率的大小.
解答 解:2s内的位移x2=(6×2-2×8)-0=-4m,则平均速度$\overline{v}=\frac{{x}_{2}}{t}=\frac{-4}{2}m/s=-2m/s$.
由v=(6-6t2)m/s知,质点速度减为零的时间t=1s,则1s内的位移大小x1=(6×1-2×1)m=4m,因为2s内的位移为-4m,则第2s内的位移大小x2=8m,
则路程s=x1+x2=4+8m=12m,则平均速率v=$\frac{s}{t}=\frac{12}{2}m/s=6m/s$.
故选:A.
点评 解决本题的关键知道平均速度和平均速率的区别,平均速率等于路程与时间的比值,需注意质点是否反向.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
16. 三根完全相同的长直导线互相平行,通以大小和方向都相同的电流.它们的截面处于一个正方形abcd的三个顶点a、b、c处,如图所示.已知每根通电长直导线在其周围产生的磁感应强度与距该导线的距离成反比,通电导线b在d处产生的磁场其磁感应强度大小为B,则三根通电导线产生的磁场在d处的总磁感应强度大小为( )
三根完全相同的长直导线互相平行,通以大小和方向都相同的电流.它们的截面处于一个正方形abcd的三个顶点a、b、c处,如图所示.已知每根通电长直导线在其周围产生的磁感应强度与距该导线的距离成反比,通电导线b在d处产生的磁场其磁感应强度大小为B,则三根通电导线产生的磁场在d处的总磁感应强度大小为( )
 三根完全相同的长直导线互相平行,通以大小和方向都相同的电流.它们的截面处于一个正方形abcd的三个顶点a、b、c处,如图所示.已知每根通电长直导线在其周围产生的磁感应强度与距该导线的距离成反比,通电导线b在d处产生的磁场其磁感应强度大小为B,则三根通电导线产生的磁场在d处的总磁感应强度大小为( )
三根完全相同的长直导线互相平行,通以大小和方向都相同的电流.它们的截面处于一个正方形abcd的三个顶点a、b、c处,如图所示.已知每根通电长直导线在其周围产生的磁感应强度与距该导线的距离成反比,通电导线b在d处产生的磁场其磁感应强度大小为B,则三根通电导线产生的磁场在d处的总磁感应强度大小为( )| A. | 2B | B. | 3B | C. | $\frac{3\sqrt{3}}{2}B$ | D. | 3$\sqrt{2}B$ |
6.一物体以初速度v0、加速度a做匀加速直线运动,若物体从t时刻起,加速度a逐渐减小至零,则物体从t时刻开始( )
| A. | 速度开始减小,直到加速度等于零为止 | |
| B. | 速度继续增大,直到加速度等于零为止 | |
| C. | 物体做减速运动,直到加速度等于零为止 | |
| D. | 位移均匀增大,直到加速度等于零为止 |
13. 如图,质量为m的小物块P位于斜面Q上,Q与水平面的夹角为θ,不计一切摩擦,小物块P从静止开始沿斜面下滑的过程中( )
如图,质量为m的小物块P位于斜面Q上,Q与水平面的夹角为θ,不计一切摩擦,小物块P从静止开始沿斜面下滑的过程中( )
 如图,质量为m的小物块P位于斜面Q上,Q与水平面的夹角为θ,不计一切摩擦,小物块P从静止开始沿斜面下滑的过程中( )
如图,质量为m的小物块P位于斜面Q上,Q与水平面的夹角为θ,不计一切摩擦,小物块P从静止开始沿斜面下滑的过程中( )| A. | 斜面给P的支持力为mgcosθ | |
| B. | 物块P对斜面做正功 | |
| C. | 物块P的机械能守恒 | |
| D. | 斜面对P的弹力方向不垂直于接触面 |
10.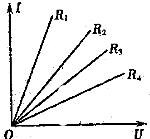 如图所示,是四只电阻的伏安特性曲线,当这四只电阻R1、R2、R3、R4并联起来使用时,通过各个电阻的电流分别是I1、I2、I3、I4,则其大小顺序为( )
如图所示,是四只电阻的伏安特性曲线,当这四只电阻R1、R2、R3、R4并联起来使用时,通过各个电阻的电流分别是I1、I2、I3、I4,则其大小顺序为( )
 如图所示,是四只电阻的伏安特性曲线,当这四只电阻R1、R2、R3、R4并联起来使用时,通过各个电阻的电流分别是I1、I2、I3、I4,则其大小顺序为( )
如图所示,是四只电阻的伏安特性曲线,当这四只电阻R1、R2、R3、R4并联起来使用时,通过各个电阻的电流分别是I1、I2、I3、I4,则其大小顺序为( )| A. | I1>I2>I3>I4 | B. | I4>I3>I2>I1 | C. | I1=I2=I3=I4 | D. | I2>I4>I3>I1 |
11.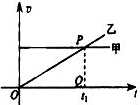 甲、乙两车在公路上沿同一方向做直线运动,它们的v-t图象如图所示,两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,则下面四组t′和d的组合不可能是( )
甲、乙两车在公路上沿同一方向做直线运动,它们的v-t图象如图所示,两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,则下面四组t′和d的组合不可能是( )
 甲、乙两车在公路上沿同一方向做直线运动,它们的v-t图象如图所示,两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,则下面四组t′和d的组合不可能是( )
甲、乙两车在公路上沿同一方向做直线运动,它们的v-t图象如图所示,两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,则下面四组t′和d的组合不可能是( )| A. | t′=t1,d=S | B. | t′=$\frac{1}{2}$t1,d=$\frac{1}{4}$S | C. | t′=$\frac{1}{2}$t1,d=$\frac{1}{2}$S | D. | t′=$\frac{1}{2}$t1,d=$\frac{3}{4}$S |
 如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点且RA=RC=2RB,则三质点的线速度之比VA:VB:VC=2:1:1;角速度之比ωA:ωB:ωC=2:2:1.
如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点且RA=RC=2RB,则三质点的线速度之比VA:VB:VC=2:1:1;角速度之比ωA:ωB:ωC=2:2:1. 如图所示,固定于同一条竖直线上的A、B是两个等量异种电荷的点电荷,电荷电量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形,另有一个带电小球P,质量为m、电荷量为+q(可视为质点),被长为L的绝缘轻质细线悬挂于O点,O点在C点正上方.现在把小球P拉到M点,使细线水平绷直且与A、B、C处于同一竖直面内,并由静止开始释放,小球P向下运动到最低点C时,速度为v,已知静电力常量为k,若取D点的电势为零,重力加速度为g,试求:
如图所示,固定于同一条竖直线上的A、B是两个等量异种电荷的点电荷,电荷电量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形,另有一个带电小球P,质量为m、电荷量为+q(可视为质点),被长为L的绝缘轻质细线悬挂于O点,O点在C点正上方.现在把小球P拉到M点,使细线水平绷直且与A、B、C处于同一竖直面内,并由静止开始释放,小球P向下运动到最低点C时,速度为v,已知静电力常量为k,若取D点的电势为零,重力加速度为g,试求: