题目内容
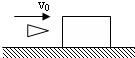
如图所示,固定的光滑的弧形轨道末端水平,固定于水平桌面上,B球静止于轨道的末端.轨道最高点距轨道末端高度及轨道末端距地高度均为R.A球由轨道最高点静止释放,A球质量为2m,B球质量为m,A、B均可视为质点,不计空气阻力及碰撞过程中的机械能的损失.求:A、B两球落地点的水平距离?


A球下滑过程到与B球碰撞前机械能守恒,则有
2mgR=
(2m)v2
解得,v=
A、B两球发生弹性碰撞,动量守恒、机械能守恒,则
2mv=2mvA+mvB
(2m)v2=
(2m)
+
m
解得,vA=
,vB=
碰撞后两球都做平抛运动,
则 R=
gt2
A的水平位移为xA=vAt,B的水平位移为xB=vBt,则A、B两球落地点的水平距离为△x=xB-xA,
代入解得,△x=2R.
答:A、B两球落地点的水平距离为2R.
2mgR=
| 1 |
| 2 |
解得,v=
| 2gR |
A、B两球发生弹性碰撞,动量守恒、机械能守恒,则
2mv=2mvA+mvB
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2A |
| 1 |
| 2 |
| v | 2B |
解得,vA=
| 1 |
| 3 |
| 2gR |
| 4 |
| 3 |
| 2gR |
碰撞后两球都做平抛运动,
则 R=
| 1 |
| 2 |
A的水平位移为xA=vAt,B的水平位移为xB=vBt,则A、B两球落地点的水平距离为△x=xB-xA,
代入解得,△x=2R.
答:A、B两球落地点的水平距离为2R.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目


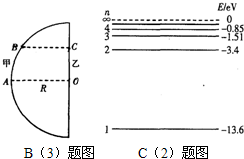
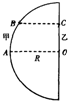 (3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?
(3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?