Question

【题目】如图所示，横截面是直角三角形ABC的三棱镜对红光的折射率为n1 ， 对紫光的折射率为n2 ， 一束很细的白光由棱镜的一个侧面AB垂直射入，从另一个侧面AC折射出来．已知棱镜顶角∠A＝30°，AC边平行于光屏MN ， 且与光屏的距离为L ．
（1）画出白光通过棱镜折射的光路图(出射光线画两条边缘光线，并指明其颜色)．
（2）求在光屏MN上得到的可见光光谱的宽度d ．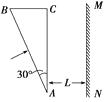

Answer 1

【答案】
（1）

由于光线垂直AB面入射，故在AB面上光线不偏折．在AC面，设红光折射角为β1，紫光折射角为β2，由于n2＞n1，所以紫光偏折角度将大于红光，故β2＞β1，光谱上方为紫光，下方为红光．光路图如图所示．

（2）

由折射定律得：n1sin 30°＝sin β1，n2sin 30°＝sin β2，则sin β1＝，sin β2＝．

MN上可见光光谱的宽度：

d＝L(tan β2－tan β1)＝L

＝L．

【解析】光垂直AB面射入，在AB面上不发生偏折，射到AC面上，入射角为 ，根据三棱镜对红光的折射率为 ，对紫光的折射率为 ．运用折射定律求出折射角，再根据几何关系求出可见光谱的宽度。